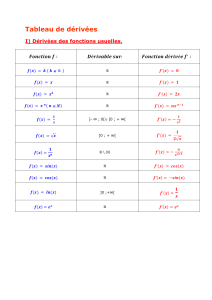
ch4: application de la dérivation

1S-Chapitre 4: applications de la dérivation
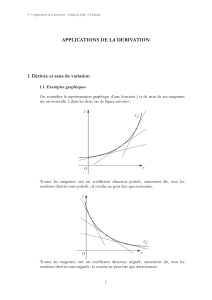
I Observation du lien dérivée - variations d’une fonction (livre p.89)
I-A Observation avec geogebra : soit
f(x) = 2x3 − 3x2 − 12x + 5 définie
sur R
1. Observation et conjecture :
a) Soit Cf la représentation graphique de f .
Compléter les pointillés concernant les coefficients directeurs des 4 tangentes prises en
exemple sur le schéma ci-contre.
Conjecturer alors le signe de f 0 (x) sur les
intervalles suivants :
• ]−∞; · · · · · · · · · · · · ] : . . . . . . . . . . . . .
• [· · · · · · · · · ; · · · · · · · · · ] : . . . . . . . . . . . . .
• [· · · · · · · · · ; · · · · · · · · · [ : . . . . . . . . . . . . .
b) Émettre une conjecture sur le lien signe de f 0 (x)
et sens de variations de f :
2. Étude du signe de f 0 x) :
a) Calculer f 0 (x) : f (x) est . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
f 0 (x) = . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
b) Étude du signe de f 0 (x) :
x
f 0 (x)
−∞
······
······
0
0
+∞
I-B Signe de la dérivée et extremum
1. Détermination du minimum de la fonction S :
a) Détermination de la fonction S :
– (Aire de AM P ) calculer h, en utilisant la figure :
h2 = · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
···············
Donc :h = · · · · · · · · · · · · · · · · · · ;AAPM =
······
0
– (Aire de MQB ) calculer h , en utilisant la figure :
h02 = · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
···············
Donc :h0 = · · · · · · · · · · · · · · · · · · ;AMQB =
······
Mme Bessaguet
Page 1 sur 3
Donc : S(x) = . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
10 septembre 2014
1S-Chapitre 4: applications de la dérivation
b) Écrire S(x) sous forme canonique :S(x) = . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ; Minimum de S sur [0; 10] : . . . . . . . . . . . . . . . . . . . .
2. Lien avec la fonction dérivée S 0 :
x
a) S 0 (x) = . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
S 0 (x)
−∞
······
+∞
0
b) Conjecture sur le lien entre la présence d’un minimum et le signe de S 0 (x) : . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
........................................................................................................................
........................................................................................................................
II Fonction dérivée et variations
II-A Du sens de variations au signe de la dérivée
1. Théorème :
Soit f
• Si f
• Si f
• Si f
une fonction dérivable sur un intervalle I :
est croissante sur I , alors pour tout x de I : f 0 (x) ≥ 0
est décroissante sur I , alors pour tout x de I : f 0 (x) ≤ 0
est constante sur I , alors pour tout x de I : f 0 (x) = 0
2. Application :soit f une fonction dérivable sur [−4; 6] dont la courbe représentative est donnée ci-contre. Donner le signe de la dérivée en complétant d’abord le tableau de variations ci-dessous.
x
6
−4
S(x)
S 0 (x)
Commentaires :
II-B Du signe de la dérivée au sens de variations
1. Théorème réciproque :
Soit f une fonction dérivable sur un intervalle I :
• Si pour tout x de I : f 0 (x) ≥ 0 alors f est croissante sur I .
• Si pour tout x de I : f 0 (x) ≤ 0 alors f est décroissante sur I .
• Si pour tout x de I : f 0 (x) = 0 alors f est constante sur I .
2. Application : + no 18 p 96
2
3
Soit la fonction f définie sur R par : f (x) = x 3 + x 2 − 2x − 1
3
2
a) Calculer f 0 (x) :
f 0 (x) = . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
b) Compléter le tableau ci-contre dans lequel vous ferez figurer le signe de f 0 (x), et en déduire les variations de
f.
Mme Bessaguet
Page 2 sur 3
10 septembre 2014
1S-Chapitre 4: applications de la dérivation
Étude de signe de f0 (x) :
x
−∞
+∞
0
f (x)
f (x)
c) En déduire l’existence éventuel d’extrema locaux :
...................................................................
II-C Extremum local d’une fonction
1. Définition : soit f une fonction dérivable sur un intervalle I et c un nombre réel de I .
•Dire que f (c) est un maximum ( resp. . . . . . . . . . . . . . . . . . . . .) local de f signifie qu’il existe un intervalle ouvert
J ( J ⊂ I , x ∈ J ) tel que : f (x) · · · · · · · · · · · · · · · f (c) (resp.f(x) · · · · · · · · · · · · · · · f(c) )
•un extremum local est soit un maximum local, soit un minimum local.
2. Propriété : Pour une fonction dérivable f , s’il existe un extremum local en c, alors : f 0 (c) = · · · · · · · · ·
3. Application : no 25, 27, 28 et 30 p 97.
Mme Bessaguet
Page 3 sur 3
10 septembre 2014