8 applicationderivation

8. APPLICATIONS DE LA DERIVATION
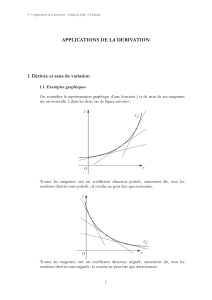
1. Lien entre signe de la dérivée et sens de variation.
A. Fonction constante sur un intervalle :
Théorème : Si f est dérivable sur un intervalle I et si la dérivée f ’est sur I ,
alors la fonction f est sur I.
B. Fonction dérivable et monotone sur I :
L’observation du coefficient directeur de la tangente à partir d’exemples, nous a permis de
déduire les résultats suivants :
Théorème 1 : Si f est dérivable sur un intervalle I et si la dérivée f ’est
sur I , alors la fonction f est sur I.
Théorème 2 : Si f est dérivable sur un intervalle I et si la dérivée f ’est
sur I , alors la fonction f est sur I.
Les propriétés réciproques sont admises.
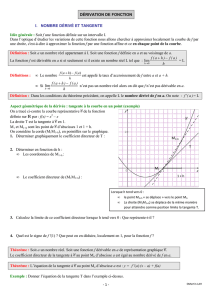
2. Extremum local d’une fonction :
Propriété ( admise ) : f est une fonction dérivable sur un intervalle I et x0 un nombre réel de I.
Si f ( x0 ) est un extremum local de f alors f ’(x0) = 0
Remarques : - au point d’abscisse x0 , la tangente à la courbe est « horizontale »
- La réciproque de cette propriété est fausse.
Propriété ( admise ) : f est une fonction dérivable sur un intervalle I et x0 un nombre réel de I ( qui n’est pas
une extrémité de I )
Si f ’ s’annule en x0 , alors f (x0 ) est
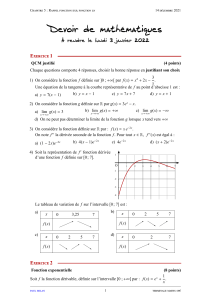
3. Exemple : On se propose d’étudier le sens de la fonction f définie sur [ –3 ; 2 ] par :
f(x) = x 3 – 3x + 2 .
Les variations de f sont présentées dans son tableau de variation :
x
– 3 –1 1 2
Signe de f ’(x)
Variation de f