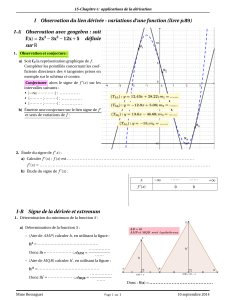
TS-Dérivation continuité

TS - Dérivation et continuité Cours
DÉRIVATION ET CONTINUITÉ
1 Dérivation
Propriété 1.1 :Dérivées
des fonctions usuelles
(rappel)
f(x)f′(x)
k(constante) 0
x1
x22x
x33x2
xn,n∈N∗nxn−1
1
x−1 x2
√x1
2√x
Propriété 1.2 :Opérations sur les fonctions (rappel)
Soient uet vdeux fonctions dérivables sur un intervalle I et k∈R.
Opérations Fonction fDérivée f′
Somme u+v u′+v′
Multiplication par une constante k u k u′
Produit uv u′v+uv′
Inverse 1
u−u′ u2
Quotient u
v
u′v−uv′
v2
Propriété 1.3 :Équation d’une tangente (rappel)
Soit fune fonction définie et dérivable sur I et a∈I.
La tangente en aà la courbe représentative de fa pour équation y=f′(a)(x−a) + f(a).
Propriété 1.4 :Dérivée de la racine carrée d’une fonction
Soit uune fonction définie, dérivable et strictement positive sur un intervalle I.
Alors la fonction définie sur I par : x7→ qu(x) est dérivable sur I et (√u)′=u′
2√u
Propriété 1.5 :Dérivée de la puissance d’une fonction
Soit uune fonction définie et dérivable sur un intervalle I. Soit n∈Z∗.
Alors la fonction définie sur I par : x7→ (u(x))nest dérivable sur I et (un)′=n u′un−1
Preuve : On considère deux cas : d’abord npositif, puis nnégatif.
– Si n∈N∗, on va raisonner par récurrence.
Initialisation : Pour n= 1, on a (u1)′=u′et 1 u′u1−1=u′u0=u′×1 = u′.
On a bien (u1)′= 1 u′u1−1et donc la propriété est vraie au rang n= 1.
Hérédité : On suppose que la propriété est vraie pour un certain rang navec n∈N∗.
(un+1)′= (un×u)′= (un)′×u+un×u′.
Or d’après l’hypothèse de récurrence, (un)′=n u′un−1.
Donc (un+1)′=n u′un−1×u+un×u′=n u′un+u′un= (n+ 1)u′un.
La propriété est donc vraie au rang n+ 1.
Conclusion : Donc pour tout n∈N∗, on a (un)′=n u′un−1.
– Si nest négatif, on pose m=−n. On a alors mqui est positif.
Ainsi un=1
u−n=1 um
et (un)′=−(um)′
(um)2=−m u′um−1
u2m=−m u′um−1−2m=−m u′u−m−1=n u′un−1
1

TS - Dérivation et continuité Cours
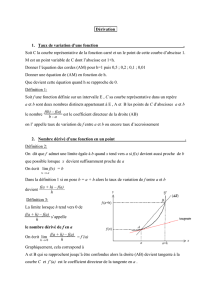
Définition 1.1 :Nombre dérivé (rappel)
Soit fune fonction définie sur un intervalle I. Soient (x0, h)∈R2.
fest dérivable en x0si et seulement si
f(x0+h)−f(x0)
htend vers un nombre réel quand htend vers 0.
Dans ce cas, ce nombre réel est appelé nombre dérivé de fen x0,
noté f′(x0).
Si fest dérivable en x0, on a alors lim
h→0
f(x0+h)−f(x0)
h=f′(x0).
x0x
hx0+h
C
1
1
O
×
A
×M
Propriété 1.6 :Dérivée de x7→ f(ax +b)
Soit fune fonction dérivable sur un intervalle I.
Soient (a, b)∈R2et J l’intervalle formé des réels xtels que ax +b∈I.
Soit la fonction g:x7→ f(ax +b).
Alors gest dérivable sur J et g′(x) = a×f′(ax +b) .
Preuve : Soient (x0, h)∈R2tels que x0∈Jet x0+h∈J.
g(x0+h)−g(x0)
h=f(a(x0+h) + b)−f(ax0+b) h=a×f(ax0+ah +b)−f(ax0+b) ah
On pose X0=ax0+bet H=ah. On obtient alors g(x0+h)−g(x0)
h=a×f(X0+H)−f(X0) H.
Quand htend vers 0, H=ah tend aussi vers 0.
De plus, comme x0∈Jalors X0=ax0+b∈Iet donc fest dérivable en X0,
et lim
H→0
f(X0+H)−f(X0)
H=f′(X0).
Finalement, lim
h→0
g(x0+h)−g(x0)
h= lim
H→0a×f(X0+H)−f(X0)
H=af′(X0) = af ′(ax0+b).
Ainsi gest dérivable sur J et pour tout x∈J,g′(x) = a×f′(ax +b).
2 Continuité
Définition 2.1 : Soit fune fonction définie sur un intervalle [a, b] avec aet bdeux nombres réels.
On dit que fest continue sur [a, b] si on peut tracer sa courbe représentative sans lever le crayon .
Propriété 2.1 : Soit fune fonction définie sur un intervalle [a, b] avec aet bdeux nombres réels.
Si fest dérivable sur [a, b] alors fest continue sur [a, b].
Propriété 2.2 :
– Les fonctions usuelles (polynômes, fonctions rationnelles, racine carrée) sont continues sur
chaque intervalle de leur ensemble de définition.
– Les fonctions construites à partir de fonctions continues par somme,produit,quotient ou com-
position, sont continues sur chaque intervalle où elles sont définies.
2

TS - Dérivation et continuité Cours
Exemple 2.1 :
a) La fonction carrée x7→ x2est continue sur R.
5
123−1−2−3
b) La fonction rationnelle x7→ 3x+ 2
5x−1est continue sur
les intervalles −∞;1
5et 1 5; +∞.
10
−10
1 2 3−1−2−3
c) La fonction partie entière est définie sur Rmais n’est
pas continue sur R. En revanche, elle est continue sur
tout intervalle de la forme [k, k + 1[ avec k∈Z.
1
2
−1
−2
1234−1−2
3 Théorème des valeurs intermédiaires
Théorème 3.1 :Théorème des valeurs intermédiaires
Soit fune fonction définie sur [a, b] et k∈R.
Si (fest continue sur [a, b]
kest compris entre f(a) et f(b),
alors il existe (au moins) un nombre αappartenant à [a, b] tel que
f(α) = k.
f(a)
k
f(b)
ab
Cf
× × ×
Propriété 3.1 :Cas d’une fonction strictement monotone
Soit fune fonction définie sur [a, b] et k∈R.
Si 
fest continue sur [a, b]
fest strictement monotone sur [a, b]
kest compris entre f(a) et f(b)
,
alors il existe un unique nombre αappartenant à [a, b] tel que f(α) = k.
Cf
a α b
f(a)
k
f(b)
Exemple 3.1 : Soit fla fonction définie sur Rpar f(x) = 2x3−5x2−7x−1.
Montrer que l’équation f(x) = −10 admet une unique solution αsur [0; 2] et déterminer une valeur
approchée de αà 10−2près.
3