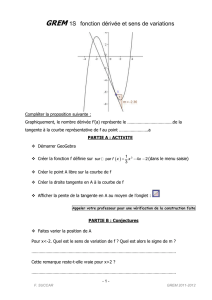
DERIVATION NOTIONS DE BASE • f `(a) est le nombre dérivé de f

DERIVATION
NOTIONS DE BASE
• f '(a) est le nombre dérivé de f en a signifie : 0
( ) ( ) ( ) ( )
'( ) lim lim
x a h
f x f a f a h f a
f a
x a h
→ →
− + −
= =
−
• On dit que
'( )( ) ( )
f a x a f a
− +
est la meilleure approximation affine de f en a.
• f ' (a) est le coefficient directeur de la tangente T à la courbe Cf en son point d'abscisse a.
• Equation de cette tangente T :
(
)
(
)
(
)
'
y f a x a f a
= − +
FORMULAIRE DE DERIVATION (n∈
∈∈
∈IN*)
f(x) k (cte) x
2
x
n
x
1
x
1
n
x
x
f '(x) 0 1 2x
1
n
nx
−
2
1
x
−
1
n
n
x
+
−
1
2
x
f ku u + v uv
1
v
u
v
f ' ku’ u’+ v’ u’v + uv’
2
'
v
v
−
2
' '
u v uv
v
−
VARIATIONS D’UNE FONCTION DERIVABLE SUR UN INTERVALLE (principe de Lagrange).
Soit f dérivable sur un intervalle I.
• si f ' > 0 sur I, sauf en des valeurs isolées de I où f ' = 0, alors f est strictement croissante sur I.
• si f ' < 0 sur I, sauf en des valeurs isolées de I où f ' = 0, alors f est strictement décroissante sur I.
• si f ' = 0 sur I, alors f est constante sur I.
EXTREMUM
Soient f dérivable sur un intervalle I ouvert et a un réel de I.
f admet un extremum en a sur I si et seulement si f ' s’annule en changeant de signe en a.