Document

7
Fonction Logarithme
Népérien
CHAPITRE
John NAPIER 1 550-1 617
John NAPIER, connu sous le nom francisé de NEPER était un mathématicien écossais,
plus connu a ses débuts pour ses attaques virulentes contre le catholicisme que ses
travaux mathématiques. Ce n’est que peu de temps avant sa mort, qu’en 1614, il mis
au point sa découverte des logarithmes, par une approche cinématique. Cette décou-
verte lui permis de publier la même année une table des logarithmes des sinus d’angles
croissant de minutes en minutes. De telles tables de logarithmes ont été utilisées jus-
qu’au XX ième siècle avant l’avènement des calculatrices de poche. Des mathémati-
ciens de A à Z.
B. HAUCHECONE et D.SURATTEAU aux éditions ellipses

Sommaire
0 Généralités
0.1 Programme de la classe de Première S
0.2 Programme de la classe de Terminale S
1 Fonction logarithme népérien
1.1 Définitions et premières propriétés
a) Définition
b) Premières propriétés
c) Lien graphique entre les fonctions exponentielle et logarithme népérien
1.2 Propriétés
a) Sens de variations et conséquences
b) Limites aux bornes
1.3 Tableau de variations et applications
a) Tableau de variations
b) Représentation graphique
c) Exercice
2 Propriétés de la fonction logarithme népérien
2.1 Propriétés algébriques
a) Logarithme népérien d’un produit
2.2 Compléments sur les limites et la dérivation
a) Autres limites
b) Dérivée de ln(u(x))
2.3 Fonction logarithme décimal et applications
a) Introduction
b) Définition
c) Propriétés
d) Exemples d’interventions
3 Résumé du cours
4 Démonstrations du cours
5 Exercices
294 Sommaire chapitre 7 Francis CORTADO

Généralités
0
01Programme de la classe de Première S
Ne figure pas au programme de la classe de Première S
02Programme de la classe de Terminale S
Comme dans les classes précédentes, l’activité mathématique est motivée par la résolution de
problèmes. L’ensemble des fonctions mobilisables est élargi par l’introduction de la fonction loga-
rithme.
L’acquisition d’automatismes de calcul demeure un objectif du programme, cependant, dans le
cadre de la résolution de problèmes, on a recours si besoin à un logiciel de calcul formel ou scienti-
fique.
CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES
Fonction x7−→ln(x) Connaître le sens de variation,
les limites et la représentation
graphique de la fonction loga-
rithme népérien.
On peut introduire la fonction logarithme
népérien grâce aux propriétés de la fonc-
tion exponentielle ou à partir de l’équa-
tion fonctionnelle.
Relation fonctionnelle,
dérivée.
• Utiliser, pour aréel stricte-
ment positif et bréel, l’équiva-
lence
lna=b⇐⇒ a=eb
• Utiliser la relation fonction-
nelle pour transformer une
écriture.
• Connaître et exploiter
lim
x→+∞
lnx
x=0
On souligne dans les cadres algébrique
et graphique que les fonctions loga-
rithme népérien et exponentielle sont ré-
ciproques l’une de l’autre.
Tout développement théorique sur les
fonctions réciproques est exclu.
On fait le lien entre le nombre dérivé de la
fonction logarithme en 1 et la limite en 0
de ln(1+x)
x
On évoque la fonction logarithme déci-
mal pour son utilité dans les autres dis-
ciplines.
[SI] Gain lié à une fonction de transfert.
[SPC] Intensité sonore, magnitude d’un
séisme, échelle des pH.
Équations fonctionnelles.
Francis CORTADO Sommaire chapitre 7 295

Fonction logarithme népérien
1
11Définitions et premières propriétés
a) Définition
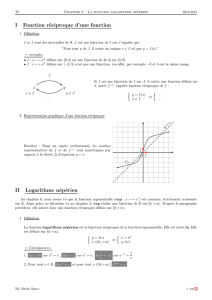
On a vu dans le chapitre V, que pour tout réel kstrictement positif l’équation ex=kadmet
une solution unique appelée logarithme népérien de ket notée ln(k).
Cette correspondance qui à k>0 associe ce nombre réel est appelée fonction logarithme népé-
rien.
x
y
1
1
0ln(k)
y=k
y=exp(x)
On appelle fonction logarithme népérien, la fonction notée "ln" qui à xstrictement positif
associe l’unique solution de l’équation
ey=x
Définition 1
Remarque.
L’adjectif "népérien" vient du nom du mathématicien anglais John NAPIER (1550−1617)
La fonction logarithme népérien permet donc de déterminer l’antécédent d’un réel stricte-
ment positif pour la fonction exponentielle.
On dit que les fonctions exponentielle et logarithme népérien sont réciproques.
Exemple.
Puisque e0=1 on a ln(1) =0, et de même puisque e1=eil vient ln(e)=1
De la définition il résulte les propriétés suivantes vues lors de l’étude de la fonction exponen-
tielle.
296 Sommaire chapitre 7 Francis CORTADO

b) Premières propriétés
Soient aet bdeux réels strictement positifs et soit kun réel quelconque.
a. Le domaine de définition de la fonction ln est l’intervalle ]0, +∞[
b. ln(a)=k⇔a=ek
c. ln(a)=ln(b)⇔a=b
d. ln(a)>k⇔a>ek
e. ln(a)>ln(b)⇔a>b
Propriété 1
Comme lors de l’étude de la fonction exponentielle, ces propriétés vont nous permettre de
résoudre des équations ou inéquations.
Exercice 1
Résoudre dans Rles équations ou inéquations suivantes
1. ln(x)=5 ; ln(2x+1) =3 ; ln2(x)+ln(x)−2=0
2. ln(x)<3 ; ln(2−x)>3 ; ln(−2x+7) 6−1
Solution
1.
• Pour x>0, lnx=5⇐⇒ x=e5
• Pour x>−1
2, ln(2x+1) =3⇐⇒ 2x+1=e3⇐⇒ x=e3−1 2
• Pour x>0, ln2(x)+ln(x)−2=0⇐⇒ X2+X−2=0 avec X=lnx.
Cette dernière équation admet comme solution X1=1 et X2=−2, ce qui donne
lnx=1 ou lnx= −2⇐⇒ x=eou x=e−2
2.
• Pour x>0, lnx<3⇐⇒ x<e3.
L’ensemble des solutions est donc l’intervalle ¤0, e3£
• Pour x<2, ln(2−x)<3⇐⇒ 2−x<e3⇐⇒ x>2−e3.
L’ensemble des solutions est donc l’intervalle ¤2−e3, 2£
• Pour x67
2, ln(−2x+7) 6−1⇐⇒ −2x+76e−1⇐⇒ x>−e−1−7 2.
L’ensemble des solutions est donc l’intervalle ·−e−1−7
2,7 2·
La propriété 1 b. admet la conséquence immédiate suivante, également rencontrée lors de
l’étude de la fonction exponentielle
a. Soit xun réel strictement positif
eln(x)=x
b. Soit xun réel quelconque
ln¡ex¢=x
Conséquences 1
Francis CORTADO Sommaire chapitre 7 297