ln - WordPress.com

TS1 année 2012/2013 mathématiques
CHAPITRE 8
La fonction logarithme népérien (ln)
I – Existence de la fonction logarithme népérien.
1- Définition du logarithme d'un nombre réel strictement positif.
La fonction exponentielle est strictement croissante et continue sur IR et à valeurs dans IR+*
Soit a un réel tel que a > 0. D'après le corollaire du théorème des valeurs intermédiaires appliqué à la fonction exp , il
existe un et un seul réel b tel que exp(b) = a .
DEF : pour tout nombre réel a > 0 , on appelle ln(a) l'unique nombre réel tel que exp(ln(a)) = a.
Ainsi :
eb=a
si et seulement si b = ln(a).
2- La fonction ln.
En vertu de ce qui précède on peut attribuer à tout réel x > 0 un nombre tel que exp(ln(x)) = x
La fonction qui à x associe ln(x) s'appelle la fonction logarithme népérien.
Elle est définie sur IR+* et à valeurs dans IR.
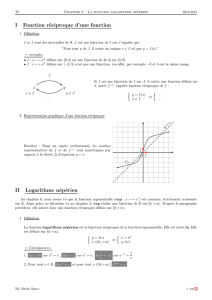
Cette fonction est la fonction réciproque de la fonction exponentielle. Elle existe puisqu'on a supposé l'existence de la
fonction exponentielle. Nous verrons plus tard grâce aux primitives comment prouver correctement l'existence des deux
fonctions.
3-Propriétés algébriques
REGLES DE CALCUL (à bien connaître).
•Soit a >0 :
eb=a
<=> b = ln(a)
•ln(1) = 0 ln(e) = 1 ln(2) ≈ 0,693 (valeur d'usage assez fréquent)
•si 0 < a < 1 alors ln(a) < 0
si 1 < a alors ln(a) > 0
•Si a >0 et b > 0 :
ln (a b)=ln (a)+ln(b)
(1)
ln (a
b)=ln(a)−ln (b)
(2)
ln (1
a)=−ln (a)
(3)
Le logarithme transforme un produit en somme, un quotient en différence et l'inverse en l'opposé.
ROC
•dem (1) :
Soient a et b deux réels strictement positifs. Il existe deux nombres réels c et d tels que
ec=a
et
ed=b
. Par propriété de la fonction exponentielle on a :
ec+d=ec.ed
donc :
ln (a b)=ln (ec.ed)=ln(ec+d)=c+d
.
Or c = ln(a) et d = ln(b) donc :
ln (a b)=ln (a)+ln(b)
•dem (3) :
On applique la règle (1) avec b = 1/a
ln (a b)=ln (a)+ln(b)
donne
ln (a.1
a)=ln(a)+ln (1 a)
donc
ln (1)=0=ln(a)+ln (1
a)
, ce qui donne la propriété (3)
•dem (2)
On applique la propriété (1) en changeant b en 1/b. On obtient :
ln (a.1
b)=ln(a)+ln (1 b)=ln(a)−ln(b)
d'après (3)

TS1 année 2012/2013 mathématiques
•Soit n est un entier naturel :
ln (an)=nln (a)
(Cette propriété est encore vraie si n est un entier relatif).
( la démonstration se fait facilement par récurrence en utilisant la règle (1) – exercice : faites la)
•Soit n un entier naturel non nul :
ln (a
1
n)= 1
nln(a)
(en particulier
ln (
√
a)= 1
2ln(a)
)
•soit a > 0
eln(a)=a
soit b un réel quelconque :
ln (eb)=b
II- Etude de la fonction ln.
•Courbe (obtenue par symétrie de la courbe de la fonction exponentielle par rapport à la première diagonale)
•Continuité.
Comme la fonction ln est définie comme la réciproque de la fonction exp qui est continue, ln est continue sur son
ensemble de définition ]0 ; + ∞[.
•Limites aux bornes de l'ensemble de définition
Par utilisation des limites connues de la fonction exp, on en déduit :
lim
x→0, x>0
ln(x)=−∞
et
lim
x→+∞
ln(x)=+∞
•Dérivabilité.
La fonction ln est dérivable sur ]0 ; + ∞[ et
ln '(x)= 1
x
pour x > 0.
ROC dem : La relation
eln(x)=x
et la formule de dérivation :
(eu)'=u ' eu
nous permettent de
calculer la dérivée de ln.
On pose u(x) = ln(x).
La dérivée de la fonction
eln(x)
pour x > 0 est :
u ' (x)eu(x)=u ' (x)eln (x)=u' (x)×x
.

TS1 année 2012/2013 mathématiques
Or
eln(x)=x
donc la dérivée de
eln(x)
est aussi la dérivée de la fonction x → x .
On obtient donc :
u ' (x)× x=(eln x)'=1
et par conséquent :
u ' (x)= 1
x
•Sens de variations
La fonction ln est strictement croissante sur ]0 ; + ∞[ puisque sa fonction dérivée est strictement positive sur cet
intervalle.
On en déduit que 0 < a < b => ln(a) < ln(b)
III – Quelques compléments...
1- formule de dérivation avec ln.
Soit u une fonction dérivable sur son ensemble de définition et telle que u(x) est toujours strictement positif.
Alors la fonction ln o u est dérivable et pour tout x appartenant à l'ensemble de définition de u :
(ln(u(x)))'=u ' (x)
u(x)
2- Une limite utile.
•
lim
x→0, x>0
ln(x+1)
x=1
dem (ROC ?) : La fonction ln est dérivable en 1. Son nombre dérivé au point 1 est égal à ln'(1) = 1/1 =1.
Par définition du nombre dérivée de ln en 1 on peut dire que
lim
x→0, x>0
ln(x+1)
x=lim
x→0, x>0
ln(x+1)−ln (1)
(x+1)−1=ln '(1)=1
3- Croissance comparée avec les fonctions puissances.
•
lim
x→+∞
ln (x)
x=0
•pour tout entier naturel n non nul :
lim
x→+∞
ln (x)
xn=0
ROC
Dem : Soit x un nombre réel positif alors :
eln(x)=x
On a donc :
ln(x)
x=ln(x)
eln(x)
.
Posons X = ln(x) on obtient :
ln(x)
x=ln(x)
eln(x)=X eX
.
Or quand x → + ∞, ln(x) → + ∞ donc X → + ∞ .
Or on sait que
lim
X→+∞
eX
X=+∞
donc
lim
X→+∞
X
eX=0
par quotient de limites.
Par conséquent :
lim
x→+∞
ln (x)
x=0
par composition de limites.
L'extension à la deuxième limite s'obtient par produit de limites en décomposant la
fonction sous la forme :
ln(x)
xn=ln(x)
x×1
xn−1
pour n > 1.