la fonction logarithme neperien

1/10
LA FONCTION LOGARITHME NEPERIEN
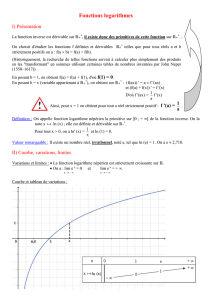
La fonction inverse x
x
1
est continue sur l’intervalle ]0, + ∞[, donc elle admet une infinité de primitives
sur cet intervalle, dont une seule s’annule en 1.
§ 1 Définition de la fonction logarithme népérien
Définition
La fonction logarithme népérien est la primitive de la fonction inverse sur ]0, + ∞[ qui prend la valeur
0 en 1.
La fonction logarithme népérien, notée ln, est définie sur ]0, + ∞[ , prend la valeur 0
en x = 1, est continue sur ]0, + ∞[ et admet pour dérivée la fonction x
x
1
§ 2 Propriétés algèbriques
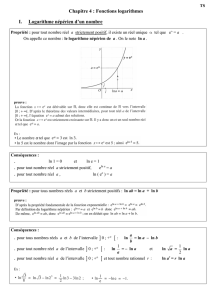
1- Relation fonctionnelle
Théorème
Pour tous les réels a et b strictement positifs, on a ln (a × b) = ln a + ln b
Démonstration :
a étant un nombre réel strictement positif quelconque et x
[;0] 
Soit f(x) = ln (ax) et g(x) = ln x
Les fonctions f et g sont dérivables sur
[;0] 
, comme composée de fonctions dérivables sur
[;0] 
et :
f '(x) = a
x
1
ax
1
et g'(x) =
x
1
f '(x) = g'(x) donc f et g sont deux primitives de
[;0]sur
x
1
x
donc f(x) = g(x) + K avec K constante réelle
f(1) = g(1) +K
d'où : ln(a) = 0 + K et f(x) = g(x) + ln(a)
ainsi : ln(ax) = lnx + lna
2- Logarithme d’un quotient
Propriétés :
Pour tous réels a > 0 et b > 0, ln
b
a
lna – lnb
Pour tout réel b > 0, ln
b
1
= - lnb
Démonstration :
. a =
b
b
a
, donc lna = ln
bln
b
a
lnb
b
a
d'après la propriété fondamentale

2/10
d'où ln
b
a
= lna – lnb
. Pour a = 1, on a : ln
b
1
= ln1 – lnb = - lnb
3- Logarithme d’un produit de nombres réels strictement positifs
Propriété :
Pour tous réels a1, a2, …, an de ] 0 ; + ∞ [,
ln ( a1 a2 … an ) = ln a1 + ln a2 + … + ln an
Démonstration :
. pour n = 2, la proposition est vraie : ln(a1a2) = lna1 + lna2, d'après la propriété fondamentale
. on suppose qu'il existe un rang k pour lequel la propriété est vraie :
hypothèse de récurrence : ln (a1a2…ak) = ln a1 + ln a2 + … + ln ak
Alors, ln (a1a2…ak+1) = ln ((a1a2…ak)ak+1) = ln (a1a2…ak) + ln ak+1, d'après la propriété précédente
D'où, ln (a1a2…ak+1) = (ln a1 + ln a2 + … + ln ak) + ln ak+1
Donc la propriété est démontrée au rang k + 1
. Les axiomes de récurrence permettent de conclure que pour tous réels a1, a2, …, an de ] 0 ; + ∞ [,
ln ( a1 a2 … an ) = ln a1 + ln a2 + … + ln an
Propriété :
Pour tout réel a de ] 0 ; + ∞ [, et tout entier relatif n, ln (an) = n ln a
Démonstration :
. dans le résultat précédent, lorsque a1 = a2 = … = an = a, on obtient : pour tout naturel n ≥ 1, pour tout a > 0, ln
an = n ln a
. et si n est strictement négatif, on écrit :
ln (an) = ln
n
a1
= - ( ln a-n)
Or – n > 0 donc ln (a-n) = -n ln a, et ln (an) = n ln a
. si n = 0, ln an = ln a0 = ln 1 = 0 et n ln a = 0 ln a = 0
4- Logarithme d’une racine carrée
Propriété :
Pour tout réel a de ] 0 ; + ∞ [, ln
a
=
2
1
ln a
Démonstration :
a =
a
a
donc, d'après la propriété fondamentale, ln a = ln
a
+ ln
a
= 2 ln
a
d'où : ln
a
=
2
1
ln a
§ 3 Etude de la fonction logarithme

3/10
1- Sens de variation de la fonction logarithme népérien sur ]0 ; + ∞[
La fonction x
xln
est définie sur ]0 ; + ∞[
La fonction x
xln
est continue sur ]0 ; + ∞[
La fonction x
xln
est dérivable sur ]0 ; + ∞[
Pour tout x de ]0 ; + ∞[, (ln x)’ =
x
1
Théorème
La fonction x
xln
est strictement croissante sur ]0 ; + ∞[
2- Résolution d’équations et d’inéquations
Théorème
Pour tous les réels a et b strictement positifs, on a : ln a < ln b si et seulement si a < b
Conséquences :
ln x < 0 si et seulement si 0 < x < 1
ln x > 0 si et seulement si x ∈ ]1 ; + ∞[
3- Limites de la fonction logarithme népérien en 0 et en + ∞
Propriétés
xlnlimetxlnlim
0x 0xx
Démonstration :
. Soit A un réel strictement positif : peut-on trouver x tel que ln x > A ?
La fonction exponentielle étant strictement croissante, pour que ln x > A, il suffit que eln x > eA , soit x > eA .
Donc
x
lim
ln x = + .
. Posons X =
x
1
On a ln X = - ln x et la limite de X lorsque x tend vers 0 par valeurs positives est + . Donc
0x 0x
lim
ln x =
X
lim
(- ln X) = -
4- Tableau de variation
x
0 + ∞
f ’(x)
+
Variation
de
f
- ∞---
+ ∞

4/10
5- Représentation graphique
Remarques :
La tangente à la courbe au point d’abscisse x = 1 est la droite d’équation y = x - 1
La courbe représentative de la fonction logarithme népérien admet l’axe des ordonnées comme asymptote
6- Autres limites
Propriétés
0)xlnx(lim0
xxln
lim
0x 0xx 
Démonstration :
 Par exemple en étudiant la fonction auxiliaire g(x) =
x
- ln x
g est dérivable sur ]0 ; + ∞[ comme somme de fonctions dérivables sur ]0 ; + ∞[
g’(x) =
x2
1
-
x
1
g’(x) =
x2 2x 
e
2 3 4 5 6 7 8 9 10 11 12-1-2-3-4
2
3
4
5
6
-1
-2
-3
-4
-5
-6
0 1
1
x
y

5/10
Sur ]0 ; + ∞[ le signe de g’(x) est le signe de
x
- 2
On résoud l’inéquation :
x
- 2 > 0
x
> 2
La fonction racine carrée est strictement croissante sur ]0 ; + ∞[ :
x > 4
donc g’(x) > 0 sur ]4 ; + ∞[ et g’(x) < 0 sur ]0 ; 4[ et g’(4) = 0
g est strictement croissante sur ]4 ; + ∞[ et g est strictement décroissante sur ]0 ; 4[
x
0 4
+ ∞
Signe de g’(x)
-
+
Variation de g
g admet sur ]0 ; + ∞[ un minimum strictement positif (2 – ln 2 ≈ 0,6)
donc pour tout x de ]0 ; + ∞[ g(x) > 0
et pour tout x de ]0 ; + ∞[ ln x <
x
pour tout x > 1 on a : 0 < ln x <
x
d’où : 0 <
xxln
<
x
x
x
1
lim
x
x
lim xx 
= 0
D’après le théorème des gendarmes :
xxln
lim
x
= 0
 En posant t =
x
1
, on a xln x =
tln
t
1
t
1
ln
t
1
Or, lorsque x tend vers 0 par valeurs positives, t tend vers + et on utilise la propriété précédente.
Approximation affine de ln(1+h) pour h proche de 0
h)h1ln(
lim0h
= 1
L'approximation affine de ln (1 + h) pour h proche de 0, associée à la fonction ln est
donnée par ln(l + h) ln l + h ln' 1, c'est-à-dire ln (1 + h) h .
Démonstration :
2 - ln 2