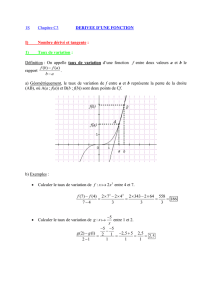
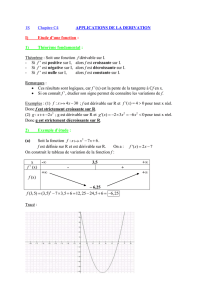
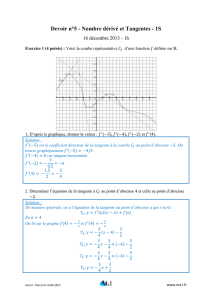
9. Dérivation des fonctions à valeurs vectorielles, arcs paramétrés

9. Dérivation des fonctions à valeurs vectorielles,
arcs paramétrés
Les fonctions étudiées dans ce chapitre sont définies sur un intervalle I(non trivial, c’est-à-dire de
longueur strictement positive) de Ret à valeurs dans un R-espace vectoriel Ede dimension finie n
(nentier, n≥2). On rappelle que les notions de limite, de continuité, de négligeabilité pour les
fonctions à valeurs dans Esont indépendantes du choix de la norme dans E.
II - Vecteur dérivé en un point, fonctions de classe C
1
1) Définitions
Définition : soit aun point de I, on dit que fest dérivable en asi et seulement si la fonction
h→ 1
h·f(a+h)−f(a)
définie sur (−a+I)\ {0}, à valeurs dans E, admet une limite finie en 0.
Cette limite est alors appelée vecteur dérivé de fen aet est notée f
′
(a).
Notations : f
′
(a)est aussi noté Df(a)ou df
dt(a).
Théorème et définition : on dit que fadmet un développement limité à l’ordre 1 en asi et seulement
s’il existe un vecteur vde Etel que :
f(a+h) =
h→0
f(a) + h.v +o(h).
Si un tel développement existe, il est unique.
Théorème : fest dérivable en asi et seulement si elle admet un développement limité à l’ordre 1 en
a, auquel cas ledit développement s’écrit :
f(a+h) =
h→0
f(a) + h.f
′
(a) + o(h).
Corollaire : toute fonction dérivable en aest continue en a(la réciproque est fausse).
Définition : soit aun point de Itel que I
′
a
=I∩[a, +∞[(resp.I
′′
a
=I∩]−∞, a]) ne soit pas réduit
au point a.
On dit que fest dérivable à droite (resp. à gauche) en asi et seulement si la restriction
de fàI
′
a
(resp. à I
′′
a
) est dérivable en a.
S’il existe, un tel vecteur dérivé s’appelle vecteur dérivé à droite (resp. à gauche) de fen
aet est notée f
′
d
(a)(resp.f
′
g
(a)).
Définition : soit Jun intervalle inclus dans I.
On dit que fest dérivable sur Jsi, et seulement si, la restriction de fàJest dérivable
en tout point de J.
Dans ce cas, f
′
:J→E, t → f
′
(t)est appelée application dérivée de fsur J.
L’application f
′
est aussi notée Dfou df
dt.
Définition : on dit que fest de classe C
1
sur Isi et seulement si fest dérivable sur Iet la fonction
dérivée f
′
est continue sur I.
On désigne par C
1
(I, E)l’ensemble des fonctions de classe C
1
sur Ià valeurs dans E.
2) Caractérisation à l’aide des composantes
Soit B= (e
1
, . . . , e
n
)une base de E,f:I→Eet (f
1
, . . . , f
n
)les fonctions coordonnées de fdans B,
∀x∈I f (x) =
n
k=1
f
k
(x).e
k
.

9. Dérivation des fonctions à valeurs vectorielles,arcs paramétrés Page 2
Théorème : soit a∈I.fest dérivable en asi et seulement si toutes les composantes f
k
de fdans la
base Bsont dérivables en a.
Dans ce cas, f
′
(a) =
n
k=1
f
′
k
(a).e
k
(autrement dit, les applications coordonnées de f
′
sont
les dérivées des applications coordonnées de f).
Dém. provient du résultat analogue sur les limites.
Conséquence : cas d’une fonction fà valeurs complexes
fest dérivable en a⇔Re fet Imfsont dérivables en a
⇔fest dérivable en a.
Dans ce cas, Df= Df,Df= D (Re f) + i.D (Imf).
Exemple :f:I→ M
n,p
(R), t → (a
i j
(t)) est dérivable sur Isi et seulement si toutes les fonctions
a
i j
sont dérivables sur I. Dans ce cas : ∀t∈I f
′
(t) = a
′
i j
(t).
3) Opérations sur les fonctions dérivables
Théorème : on désigne par D(I, E)l’ensemble des fonctions dérivables sur Ià valeurs dans E.
1) Soit (f, g)∈(D(I, E))
2
et λ∈R. Les fonctions f+get λ f sont dérivables sur Iet :
(f+g)
′
=f
′
+g
′
,(λ .f)
′
=λ. f
′
.
2) D(I, E)est un R-espace vectoriel et la dérivation est linéaire de D(I, E)dans E
I
.
C
1
(I, E)est un R-espace vectoriel.
3) Soit Jun intervalle de R. Si ϕ∈ D (J, R),f∈ D (I, E)et si ϕ(J)⊂I, alors
f◦ϕest dérivable sur Jet (f◦ϕ)
′
=ϕ
′
.f
′
◦ϕ.
4) Si ϕ∈ C
1
(J, R), f ∈ C
1
(I, E)et si ϕ(J)⊂I, alors f◦ϕ∈ C
1
(J, E).
Théorème : soit Lune application linéaire de Edans un R-espace vectoriel de dimension finie F.
Si f∈ D (I, E), alors L◦fest dérivable sur Iet (L◦f)
′
=L◦f
′
.
Si, de plus, f∈ C
1
(I, E), alors L◦fest de classe C
1
sur I.
Théorème : soient E, F, G trois R-espaces vectoriels de dimension finie, Bune application bilinéaire
de F×Gdans E,f∈ D (I, F )et g∈ D (I, G).
L’application h:t→ B(f(t), g (t)) de Idans Eest dérivable sur Iet
∀t∈I h
′
(t) = Bf
′
(t), g (t)+Bf(t), g
′
(t).
Applications :
1) Si Eest un R-espace vectoriel muni d’un produit scalaire et si fet gsont deux éléments de D(I, E),
alors les applications (f|g)et f
2
2
sont dérivables sur Iavec
(f|g)
′
=f
′
|g+f|g
′
et f
2
2
′
= 2 f|f
′
(.
2
étant la norme associée au produit scalaire).
2) Si Eest un R-espace vectoriel muni d’un produit scalaire, f∈ D (I, E)et ∀t∈I, f(t)
2
= 1, alors
pour tout élément tde I, les vecteurs f(t)et f
′
(t)sont orthogonaux.
En effet, l’application :t−→ f(t)
2
2
est constante (égale à 1) sur I, et sa dérivée est nulle sur I.
3) Si f∈ D (I, E)et ϕ∈ D (I, R), alors ϕ.f ∈ D (I, E)et (ϕ.f)
′
=ϕ
′
.f +ϕ.f
′
.
Si, de plus, ϕne s’annule pas sur I, alors 1
ϕ·fest dérivable sur Iet 1 ϕ·f
′
=1
ϕ
2
·(ϕ. f
′
−ϕ
′
. f).
(L’application : R×E→E, (λ, x)→ λ.x est bilinéaire).

9. Dérivation des fonctions à valeurs vectorielles,arcs paramétrés Page 3
4) Si Aet Bsont deux éléments de D(I, M
n
(R)), alors AB ∈ D (I, M
n
(R)) et (AB)
′
=A
′
B+AB
′
.
(L’application : (A, B)→ AB est bilinéaire sur M
n
(R)).
5) Le résultat se généralise aux applications multilinéaires, notamment au déterminant d’une famille
de nvecteurs dans une base : si Best une base de Eet si les f
k
,1≤k≤nsont napplications
dérivables de Idans E, alors
d
dtdet
B
f
1
(t), . . . , f
n
(t)=
n
k=1
det
B
f
1
(t), . . . , f
k−1
(t), f
′
k
(t), f
k+1
(t), . . . , f
n
(t).
4) Inégalité des accroissements finis (hors programme mais classique)
Soient · une norme sur E,fcontinue sur [a, b], dérivable sur ]a, b[et M≥0tel que, pour tout point
tde ]a, b[, l’on ait f
′
(t) ≤ M, alors
f(b)−f(a) ≤ M. |b−a|
Dém. On peut supposer a < b. Soit ε > 0,g:t→ f(t)−f(a) − (M+ε)tet ufixé dans ]a, b[.
La fonction gest continue sur le segment [u, b], elle admet donc un minimum atteint en un point cde
[u, b]. Montrons par l’absurde que c=b: supposons un instant c < b, alors fest dérivable en cet, par
définition de f
′
(c)et par continuité de la norme, je dispose de t∈]c, b[(suffisamment proche de c) tel
que 
1
t−c·f(t)−f(c)
−ε < 
f
′
(c)
≤M
d’où
f(t)−f(c)<(M+ε) (t−c)
mézalor par l’inégalité triangulaire
g(t)≤ f(t)−f(c)+f(c)−f(a) − (M+ε)t < g (c)
ce qui contredit la définition de c. Donc c=bet en particulier g(b)≤g(u), cela pour tout ude ]a, b[,
donc par continuité de gen a
g(b)≤g(a)c’est-à-dire f(b)−f(a) ≤ (M+ε).(b−a)
cela pour tout ε > 0, d’où le résultat en faisant tendre εvers 0.
Applications :
•Si fest continue sur I, de classe C
1
sur ˚ I,fest k-lipschitzienne sur Isi et seulement si f
′
 ≤ k;
•Si fest continue sur I, de classe C
1
sur ˚ I,fest constante sur Isi et seulement si f
′
est nulle sur ˚ I.
Attention ! Les résultats de la forme “il existe c∈]a, b[. . . ” (théorème de Rolle, théorème des
accroissements finis,. . . ) ne subsistent pas dans le cas des fonctions à valeurs vec-
torielles. Par exemple, f:t→ t−t
2
, t
2
−t
3
est dérivable de [0,1] dans R
2
, vérifie
f(0) = f(1) = (0,0) et pourtant f
′
ne s’annule pas. . .
IIII - Fonctions de classe C
k
1) Dérivées successives
Définition : on définit par récurrence les dérivées successives de f:f
(0)
=fet, pour k∈N
∗
, on dit
que fest kfois dérivable si f
(k−1)
est dérivable sur Iet on note f
(k)
=f
(k−1)
′
.
On désigne par D
k
(I, E)l’ensemble des fonctions kfois dérivables sur I.
Notations : f
(k)
= D
k
(f) = d
k
f
dx
k
.
Définition : a) Soit k∈N; on dit que fest de classe C
k
sur Isi et seulement si fest kfois dérivable
sur Iet f
(k)
continue sur I.
b) fest dite de classe C
∞
si et seulement si elle est de classe C
k
pour tout kde N,
autrement dit indéfiniment dérivable sur I.

9. Dérivation des fonctions à valeurs vectorielles,arcs paramétrés Page 4
Notations : C
0
(I, E): ensemble des fonctions continues sur Ià valeurs dans E.
C
k
(I, E): ensemble des fonctions de classe C
k
sur Ià valeurs dans Epour k∈N
∗
.
C
∞
(I, E): ensemble des fonctions de classe C
∞
sur Ià valeurs dans E.
2) Opérations algébriques — Structures
Théorème : soit k∈N,fet gdeux fonctions de Idans Eet λ∈R.
si fet gsont kfois dérivables sur I, alors λ. f +gest kfois dérivable sur Iet :
(λ .f +g)
(k)
=λ .f
(k)
+g
(k)
.
C
k
(I, E)et C
∞
(I, E)sont des sous-espaces vectoriels de C
0
(I, E).
Théorème : formule de Leibniz
Soit k∈N
∗
,f:I→Eet ϕ:I→R.
Si fet ϕsont kfois dérivables sur I, alors ϕ .f est kfois dérivables sur Iet
(ϕ. f)
(k)
=
k
j=0
k
j
ϕ
(j)
. f
(k−j)
.
Théorème : pour tout k∈N∪ {+∞},C
k
(I, R)est une R-algèbre commutative.
Théorème : composée de fonctions de classe C
k
Soit k∈N∪ {+∞} et Jun intervalle de R.
Si ϕ∈ C
k
(J, R),f∈ C
k
(I, E)et ϕ(J)⊂I, alors f◦ϕ∈ C
k
(J, E).
3) Formule de Taylor
Soient f:I→E,kfois dérivable sur I, et t∈I; la formule de Taylor en tpour les fonctions de R
dans Rfournit des développements limités de toutes les applications coordonnées de fdans une base
de E, ce qui permet d’écrire
f(t+h) =
h→0
k
j=0
h
j
j!f
(j)
(t) + oh
k
.
IIIIII - Arcs paramétrés
1) Notion d’arc paramétré
On appelle arc paramétré de classe C
k
tout couple Γ = (I, F ), où Iest un intervalle non trivial de Ret
Fune application de classe C
k
de Idans E,R-espace vectoriel de dimension 2 ou 3.
On appelle point de l’arc Γ = (I, F )tout couple (t, M)où t∈Iet M=F(t)(dit point mobile). On
parle aussi du point de paramètre t. On peut parler du point Mou du point F(t), mais attention aux
ambiguïtés en cas de point multiple (lorsque le point Mest atteint pour plusieurs valeurs de t, si F
n’est pas injective. . . )
Le support de l’arc est la courbe C={F(t), t ∈I}(la trajectoire de F(t)).
Le point (t, M)est dit point régulier de l’arc si et seulement si F
′
(t)= 0,point birégulier de l’arc si et
seulement si la famille (F
′
(t), F
′′
(t)) est libre.
L’arc est dit régulier (resp. birégulier) si et seulement si tous ses points le sont.
Un point où F
′
(t) = 0est dit point singulier, ou encore point stationnaire.
2) Demi-tangentes — Tangentes
Pour t∈I, on suppose l’existence de l’entier fondamental p= min n∈N
∗
/ F
(n)
(t)= 0.
La formule de Taylor à l’ordre pappliquée à Fen tdonne : F(t+h)−F(t) =
h→0
h
p
p!·F
(p)
(t) + o(1).
Or le vecteur F(t+h)−F(t)dirige la demi-droite F(t)F(t+h): pour tfixé et htendant vers 0
+
(resp. 0
−
), cette demi-droite a donc comme position limite la demi-droite d’origine F(t)dirigée par le
vecteur F
(p)
(t)(demi-tangente). Si la limite est identique pour htendant vers 0 de part et d’autre, on
parle de la tangente à Γen M=F(t).
En pratique, ce vecteur directeur de la tangente peut s’obtenir par calcul des dérivées successives de F,
ou encore en utilisant l’unicité des développements limités.

9. Dérivation des fonctions à valeurs vectorielles,arcs paramétrés Page 5
3) Paramétrages admissibles
Soit Γ = (I, F )un arc paramétré de classe C
k
(k≥1).
On dit que ϕest un changement de paramètre admissible sur Γsi et seulement si ϕest un
C
k
-difféomorphisme d’un intervalle Jde Rdans I(c’est-à-dire que ϕest une bijection de classe C
k
de
Jdans Idont la dérivée ne s’annule pas ; ϕ
−1
est alors une bijection de classe C
k
de Idans J).
Dans ce cas, on dit que l’arc paramétré (J, G), où G=F◦ϕest un paramétrage admissible de Γ.
Les deux arcs ont le même support, c’est la loi horaire de parcours de la trajectoire qui change.
(J, G)est dit de même orientation que Γsi et seulement si ϕest strictement croissante (on dit parfois
que l’arc (J, G)est parcouru “dans le sens des tcroissants”).
4) Caractère géométrique de certaines notions
Soit (J, G)un paramétrage admissible de Γ = (I, F ), avec G=F◦ϕ.
On vérifie facilement par récurrence que, pour n∈N
k
,t∈Iet u∈J,
t=ϕ(u)⇒Vect F
′
(t), F
′′
(t), . . . , F
(n)
(t)= Vect G
′
(u), G
′′
(u), . . . , G
(n)
(u).
À tout point (t, M)de Γ, on associe, s’ils existent, les entiers fondamentaux p, q définis par
p= min n∈N
∗
/ F
(n)
(t)= 0et q= min n > p / F
(p)
(t), F
(n)
(t)libre.
La droite M+ Vect F
(p)
(t)est la tangente en (t, M)àΓ; si t=ϕ(u),M=F(t) = G(u),pest
aussi égal à min n∈N
∗
/ G
(n)
(u)= 0et les droites M+ Vect F
(p)
(t),M+ Vect G
(p)
(u)sont
confondues : la notion de tangente est indépendante du paramétrage admissible choisi.
De même, dans le cas des courbes planes, pour la classification des points selon les parités de p, q :
•si pest impair, qpair : point ordinaire ;
•si pest impair, qimpair : point d’inflexion ;
•si pest pair, qimpair : point de rebroussement de première espèce ;
•si pest pair, qpair : point de rebroussement de seconde espèce.
De même, bien entendu, pour les notions de point régulier (p= 1), birégulier (p= 1 et q= 2).
IVIV - Courbes planes en coordonnées cartésiennes
Soit Γ = (I, F )un arc paramétré de classe C
k
,F(t)étant caractérisé, pour t∈I, par ses coordonnées
x(t), y (t)dans un repère cartésien O;
i, jde E.
1) Utilisation de m(t) = y
′
(t)
x
′
(t)
En tout point régulier (p= 1), F
′
(t)
x
′
(t)
y
′
(t)dirige la tangente et donc m(t)est le coefficient directeur
de ladite tangente.
En un point stationnaire (p > 1), la formule de Taylor donne
x
′
(t+h) =
h→0
h
p−1
(p−1)! ·x
(p)
(t) + o(1)et y
′
(t+h) =
h→0
h
p−1
(p−1)! ·y
(p)
(t) + o(1).
Par conséquent, m(t+h)−→
h→0
y
(p)
(t)
x
(p)
(t)(±∞ si x
(p)
(t) = 0, car dans ce cas y
(p)
(t)= 0).
Cette limite est encore le coefficient directeur de la tangente au point stationnaire M=F(t). Cette
remarque peut rendre service lorsque le quotient m(t)se simplifie.
Remarquons enfin que, lorsque x
′
(t)= 0,m
′
(t)est du signe de [F
′
(t), F
′′
(t)] = x
′
(t)y
′′
(t)−x
′′
(t)y
′
(t):
son annulation est une condition nécessaire et suffisante pour que F(t)ne soit pas birégulier. C’est en
particulier une condition nécessaire pour que F(t)soit un point d’inflexion.