I. Fonctions continues 1. Définition De façon intuitive : la

I. Fonctions continues
1. Définition
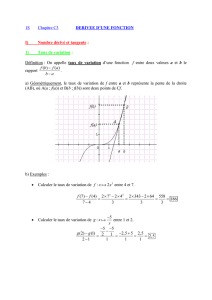
De façon intuitive : la représentation graphique d’une fonction continue se fait « sans
lever le crayon ».
De façon plus théorique : f est continue en x = a si f(a
-
) = f(a
+
) = f(a).
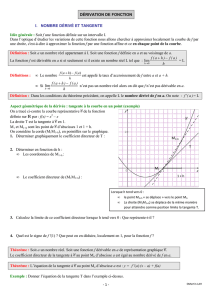
2. Le Théorème des valeurs intermédiaires
Thm : Soit f une fonction définie sur un intervalle I à valeurs dans J. Alors pour tout
réel y ∈ J, l’équation f(x) = y a des solutions sur I si f est continue sur I.
II. Fonctions dérivées
1. Dérivées de fonctions usuelles
Fonction Fonction dérivée
f(x) = a f ’(x) = 0
f(x) = ax f ’(x) = a
f(x) = ax + b f ’(x) = a
f(x) = x
n
f ’(x) = n.x
n-1
(en particulier, (x²)’ = 2x)
f(x) = 1
x
n
f ’(x) = – n
x
n+1
(en particulier, (1
x)’ = – 1 x² )
f(x) = x f ’(x) = 1
2 x (rmq : f n’est dérivable que sur ]0; + ∞[ )
2. Opérations sur les dérivées
u et v sont dérivables sur I, k ∈ IR :
*
(u + v)’ = u’ + v’
*
(k×u)’= k×u’
*
(u×v)’ = u’v + uv’
*
pour x tq v(x) ≠0 : ( u
v )’ = u’v – uv’ v²
3. Application de la dérivation
Théorème : Soit f une fonction dérivable sur I, alors si ∀ x ∈ I, on a :
f’(x) < 0 : f est décroissante sur I,
f’(x) > 0 : f est croissante sur I,
f’(x) = 0 : f est constante sur I.
4. Dérivée et tangente
Propriété : La tangente à la courbe d’équation y = f(x) en A(a ; f(a)) a pour équation :
y = f ’(a)(x – a) + f(a)
Rmq : On remarque en particulier que f ’(a) est le coefficient directeur de la tangente
en x = a.
Les Fonctions