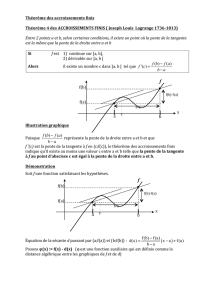
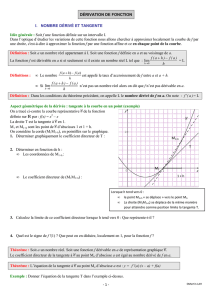
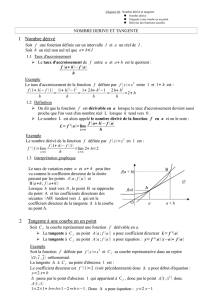
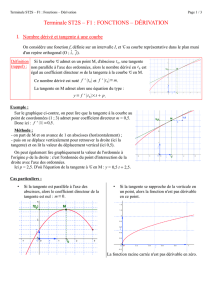
c`est la fonction dérivée de f

1S Chapitre C3 DERIVEE D’UNE FONCTION
I) Nombre dérivé et tangente :
1) Taux de variation :
Définition : On appelle taux de variation d’une fonction f entre deux valeurs a et b le
rapport
( ) ( )f b f a
ba
.
a) Géométriquement, le taux de variation de f entre a et b représente la pente de la droite
(AB), où A(a ; f(a)) et B(b ; f(b)) sont deux points de Cf.
b) Exemples :
 Calculer le taux de variation de
3
:2f x x
entre 4 et 7.
33
(7) (4) 2 7 2 4 2 343 2 64 558 186
7 4 3 3 3
ff      
 Calculer le taux de variation de
5
:gx x
entre 1 et 2.
55
(2) (1) 2,5 5 2,5
21 2,5
2 1 1 1 1
gg

2) Nombre dérivé :
En rapprochant B de A, la droite (AB) se rapproche de la tangente à Cf en A, et le taux de
variation de f se rapproche de la pente de la tangente.
En écrivant b = a + h et en rapprochant h de zéro, on a :
( ) ( ) ( ) ( )
()
f a h f a f a h f a
a h a h
qui se rapproche de la pente de la tangente en A.
Définition : Lorsque
( ) ( )f a h f a
h
admet une limite lorsque h tend vers 0, on dit que la
fonction f est dérivable en a. La limite atteinte est alors appelée nombre dérivé en a et
notée f ’(a). On note :
0
( ) ( )
'( ) lim
h
f a h f a
fa h
.
Propriété : Lorsque f ’(a) existe, alors c’est la pente de la tangente à Cf en A(a ; f(a)).
Exemple 1 : a) Calculer le taux de variation de
2
: 4 5f x x 
entre 0,5 et (0,5 + h).
b) En déduire f ’(0,5).
c) Tracer Cf et Tf (0,5).
d) Quelle est l’équation de Tf (0,5) ?
Exemple 2 : a) Calculer le taux de variation de
3
:gx x
entre -1 et (-1 + h).
b) En déduire g’(-1).
c) Tracer Cg et Tg (-1).
d) Quelle est l’équation de Tg (-1) ?
Exemple 3 : a) Calculer le taux de variation de
3
:7k x x 
entre 5 et (5 + h).
b) En déduire k’(5).
c) Tracer Ck et Tk (5).
d) Quelle est l’équation de Tk (5) ?

3) Equation de la tangente :
Théorème : Soit une fonction f et Cf sa courbe représentative. Si f ’(a) est connu, alors
l’équation de la tangente au point d’abscisse a est : y = f ’(a)(x – a) + f (a)
Preuve : Le point A appartient à la courbe, donc A (a ; f(a)).
On prend un point M (x ; y) sur Tf(a) différent de A ; (AM) a pour pente f ’(a).
On a donc :
f a y f a
x a
'( ) ( )
donc y – f(a) = f ’(a)(x – a) puis y = f ’(a)(x – a) + f (a)
4) Approximation affine d’une fonction en un point :
Erreur = distance MP
Autour du point A (a ; f(a)), la courbe Cf et la tangente Tf(a) sont très proches.
L’écart entre f(x) (valeur exacte de la fonction) et f ’(a)(x – a) + f (a) (valeur approchée de la
fonction) est d’autant plus petit que x est proche de a.
En notant h = x – a, on a :
( ) ( ) '( )f a h f a f a h  
(valable seulement pour h petit)
( ) '( )f a f a h
est l’approximation affine locale de f (a + h).
II) Fonction dérivée f ’ :
1) Définition :
Définition : Soit une fonction f définie sur un intervalle I. On dit que f est dérivable sur I si f
admet un nombre dérivé f ’(x) en tout x de I. On note f ’ la fonction ainsi obtenue : c’est la
fonction dérivée de f (« f prime »)
2) Exemple :
Soit
2
:1f x x 
définie sur . On prend une valeur
a
au hasard.
2 2 2 2 2 2
( ) ( ) [( ) 1] [ 1] 2 1 1 2 2 f a h f a a h a a ah h a ah h ah
h h h h
Donc f ’(a) = 2a (vrai pour tout valeur réelle de a !)

La fonction
2xx
donne donc f ’(x) à chaque fois.
Donc
2
:1f x x 
admet pour fonction dérivée
': 2f x x
.
3) Dérivées des fonctions usuelles :
f (x)
f ’(x)
Intervalle de validité
constante k
0
x
1
ax + b
a
x²
2x
x³
3x²
xn
, avec
n N*
nxn1
1
x
12
x
;0
ou
0;
1
xn
, avec
n N*
n
xn1
;0
ou
0;
x
1
2x
0;
sin x
(x en radians)
cos x
cos x
(x en radians)
– sin x
4) Règles de calcul :
a) Somme :
Théorème : Si u et v sont dérivables sur I, alors : (u + v)’(x) = u’(x) + v’(x)
b) Produit :
Théorème : Si u et v sont dérivables sur I, alors : (uv)’(x) = u’(x)v(x) + u(x)v’(x)

En particulier :
 (ku)’ = ku’ pour k une constante réelle.
 (u²)’ = 2uu’ (conséquence du théorème avec u = v)
Exemple : Soit
2
: (4 3)(5 )f x x x
; on pose u(x) = 4x² – 3 et v(x) = 5 – x →
2 2 2 2
'( ) ( ) '( ) '( ) ( ) (4 3)( 1) (8 )(5 ) 4 3 40 8 12 40 3f x u x v x u x v x x x x x x x x x               
c) Inverse et quotient :
Théorème : Si v est dérivable sur I avec
( ) 0vx
sur I, alors :
12
vv v
F
H
G
I
K
J
''
u
vu v uv v
F
H
GI
K
J
'' '
2
Exemples : (1) Soit
1
:37 fx x
; on pose v(x) = 3x – 7 →
22
'( ) 3
'( ) ( ) (3 7)
vx
fx v x x
(2) Soit
25
:72 gx x
; on a :
2
1
( ) 5 72 gx x
→
2 2 2 2 2
' 14 70
'( ) 5 5 (7 2) (7 2)
v x x
gx v x x
(3) Soit
32
:10 7
x
hx x
; on pose u(x) = 3x – 2 et v(x) = 10x – 7 →
2 2 2
' ' 3(10 7) 10(3 2) 1
'( ) ...
(10 7) (10 7)
u v uv x x
hx v x x
d) Dérivabilité :
Pour utiliser les formules de dérivation précédentes, il faut d’abord régler le problème de leur
validité (sur quel domaine peut-on dériver ?).
Propriété :
1) Les fonctions polynômes sont définies et dérivables sur .
2) Les fonctions rationnelles sont dérivables sur leur ensemble de définition.
Exemples de rédaction :
(1)
10 7
( ) 7 18f x x x  
; f est une fonction polynôme, donc f est définie et dérivable sur .
→
' 9 6
( ) 70 7f x x x
(2)
2
15
() 16 x gx x
; (v.i.)
2
16 0x
;
216x
; x = 4 ou x = – 4 ; donc
4;4
g
D  
g est une fonction rationnelle donc g est dérivable sur
4;4
.
u(x) = 15 – x → u’(x) = – 1
v(x) = 16 – x² → v’(x) = – 2x