angle inscrit

ANGLE INSCRIT . AU CENTRE
DESSIN SUR DR HALO / INSCEN numérotés
élèves : ANINSCEL.CHI à photocopier
I) DEFINITIONS
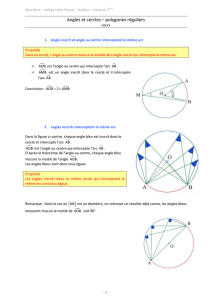
1) Angle inscrit AMB
A
M
B
O
N
l'angle ANB intercepte le même arc
Définition :Un "angle inscrit" dans un cercle est tel que :
* son sommet appartient au cercle
et * ses côtés sont sécants au cercle
*Si AMB est un angle inscrit : l'arc AB est appelé arc
intercepté par l'angle inscrit AMB
On dit : l'angle inscrit AMB intercepte l'arc AB
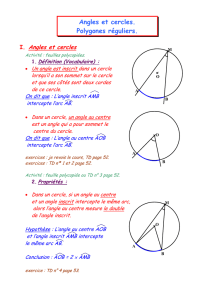
2) Angle au centre AOB
A
B
O
2}* Un angle au centre est tel que :
* son sommet est le centre du cercle
* ses côtés sont sécants au cercle
exemple : angle inscrit : AMB ANB
angle au centre : AOB , AOM
Remarque : un angle peut être
* saillant (mesure inférieure à 180°
ou * rentrant (> 180°)

A
M
B
OSaillant
Rentrant
C
* Toujours spécifier le type de l'angle (saillant-rentrant)
l'arc intercepté portera le même nom mais ne sera pas le
même
II) THEOREME DE L'ANGLE INSCRIT
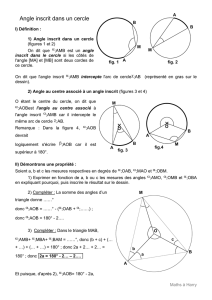
CAS 1 :
A
M
B
O
Nommer l'angle au centre :AOB
Nommer l'angle inscrit : AMB
Nature du triangle : AOM : Isocèle
(centre et 2 points du cercle)
Que peut-on dire :des angles OAM AMO : égaux
(car AOM triangle isocèle)

des angles AMO AMB : égaux
(car M,O,B sont alignés, donc même angle)
En déduire une relation entre AMB ET AOM:
La somme des angles d'un triangle est éale à 180° soit :
2AMO + AOM = 180° or M,O,B sont alignés 2AMB + AOM = 180°
(1) AMB = (180° - AOM)/2
M,O,B sont alignés AOM + AOB = 180° (angle plat )
AOM = 180° - AOB
en remplaçant dans (1) on a : AMB = (180° - (180° - AOB))/2
A
M
B
O
AMB = AOB /2 (2)
CAS 2 :
C
A
M
B
O
Exprimer CMB en fonction de COB : d'après (2) CMB = COB/2
AMC en fonction de AOC :d'après (2)AMC = AOC /2
En déduire une relation entre AMB ET AOB
AMB = AMC + CMB = AOC/2 + COB/2
AMB = AOB/2
CAS 3 :
C
A
MB
O

Exprimer AMC en fonction de AOC
d'après (2) AMC = AOC/2
BMC en fonction de BOC
d'après (2) BMC = BOC/2
En déduire une relation entre AMB ET AOB
AMB = BMC - AMC =(BOC - AOC)/2
AMB = AOB/2
Théorème de l'angle
inscrit
Dans un cercle la mesure d'un
angle inscrit est égal à la moitié
de l'angle au centre qui
intercepte le même arc
III) APPLICATIONS
EXEMPLE 1 : démontrer que AMB = ANB
A
M
B
O
N
AMB et ANB interceptent le même arc AB , d'après le théorème
de l'angle inscrit :
AMB = AOB/2 et ANB = AOB/2 soit : AMB = ANB
Théorème : Deux angles inscrits qui interceptent le même arc
ont la même mesure
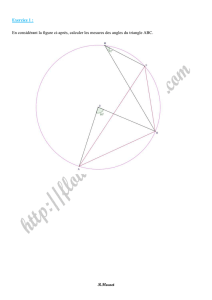
EXEMPLE 2 : ex n°1 p 151
On cherche à calculer ABC
1°) Quel est l'angle inscrit qui intercepte l'arc BC , BAC = ?
BAC intercepte l'arc BC , comme l'angle au centre interceptant
le même arc est BOC on a : BAC = BOC/2 BAC = 100°/2 = 50°,
2°) Quel est l'angle inscrit qui intercepte l'arc AB , ACB = ?
ACB intercepte l'arc AB , comme l'angle au centre BOC
on a : ACB = AOB/2 ACB = 50°/2 = 25°
3°) En déduire ABC .Dans le triangle ABC la somme des mesures

des angles est égale à 180°
ABC = 180° - (50° + 25°) = 105°