I. Définitions II. Propriétés

3ème 1
I. Définitions
1. Arcs de cercle
Sur un cercle, deux points A et B qui ne sont pas sur un même diamètre
déterminent deux arcs de cercle de longueurs différentes.
AB
est le petit arc de cercle
AB
est le grand arc de cercle.
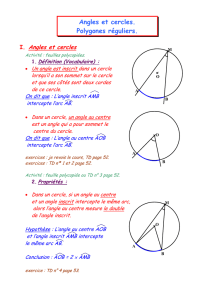
2. Angle inscrit
Un angle dont le sommet est sur le cercle et dont les côtés coupent le cercle est appelé angle
inscrit dans ce cercle.
Exemple :
AMB
est inscrit dans le cercle de centre O.
il intercepte l’arc
AB
.
3. Angle au centre
Un angle dont le sommet est le centre d’un cercle est appelé angle au centre de ce cercle.
Exemple :
AOB
est un angle au centre
Il intercepte l’arc
AB
.
II. Propriétés
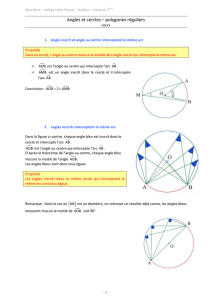
Propriété
Si dans un cercle, deux angles inscrits interceptent le même arc alors ils ont même mesure.
AMB
est inscrit dans le cercle de centre O. Il intercepte l’arc
AB
.
ANB
est inscrit dans le cercle de centre O. Il intercepte l’arc
AB
.
On a
ANB AMB

3ème 2
Propriété
Si dans un cercle un angle au centre et un angle inscrit interceptent le même arc alors la mesure de
l’angle au centre est le double de la mesure de l’angle inscrit.
AMB
est inscrit dans le cercle de centre O. il intercepte l’arc
AB
.
AOB
est un angle au centre. Il intercepte l’arc
AB
.
On a :
2
AOB AMB
III. Polygones réguliers
1. Définition
Un polygone est régulier lorsque ses côtés ont la même longueur et ses angles intérieurs ont la
même mesure.
2. Exemples
Un triangle équilatéral est un polygone régulier à trois côtés.
Un carré est un polygone régulier à quatre côtés.
Un losange n’est pas un polygone régulier. Ses angles n’ont pas la même mesure.
3. Propriété
Tout polygone régulier est inscriptible dans un cercle.
4. Propriété
Si un polygone de n côtés et de centre O est régulier alors tous les angles au centre ont la même
mesure égale à
360
n
.

3ème 3
5. Exemples :
Triangle équilatéral Carré Pentagone régulier
Hexagone régulier Octogone régulier Décagone régulier

3ème 4
Démonstration :
Soient A, B et M trois points d’un cercle (C) de centre O.
AMB
est inscrit dans le cercle de centre O. il intercepte l’arc
AB
.
AOB
est un angle au centre. Il intercepte l’arc
AB
.
1er cas : M, O et A sont alignés
[AM] est un diamètre de (C) donc
180
AOM
180
180 (1)
AOM AOB BOM
AOB BOM
AOB BOM
Or la somme des angles d’un triangle vaut 180 ° donc :
180
BOM OMB OBM
De plus OMB est isocèle en O donc :
OMB OBM
On en déduit :
2 180
180 2
BOM OMB
BOM OMB
Que l’on remplace dans (1) :
180
180 (180 2 )
180 180 2
2
2
AOB BOM
OMB
OMB
OMB
AMB
2ème cas : O est intérieur à l’angle
AMB
Soit D le point diamétralement opposé à M sur (C) .
2 2
2( )
2
AOB AOD DOB
AMD DMB
AMD DMB
AMB
2ème cas : O est extérieur à l’angle
AMB
Soit D le point diamétralement opposé à M sur (C) .
2 2
2( )
2
AOB AOD BOD
AMD BMD
AMD BMD
AMB