Angles et cercles – polygones réguliers

Marc Bizet – collège Pablo Picasso – Harfleur – classe de 3
ème
- 1 -
Angles et cercles – polygones réguliers
cours
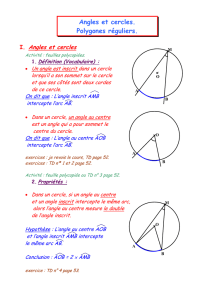
1. Angle inscrit et angle au centre interceptant le même arc
Propriété
Dans un cercle, l’angle au centre mesure le double de l’angle inscrit qui intercepte le même arc.
•
AOB
est l’angle au centre qui intercepte l’arc
AB
.
•
AMB
est un angle inscrit dans le cercle et il intercepte
l’arc
AB
.
Conclusion :
AOB 2 AMB
= ×
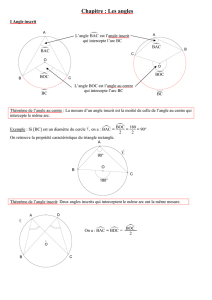
2. angles inscrits interceptant le même arc
Dans la figure ci-contre, chaque angle bleu est inscrit dans le
cercle et intercepte l’arc
AB
.
AOB
est l’angle au centre qui intercepte l’arc
AB
.
D’après le théorème de l’angle au centre, chaque angle bleu
mesure la moitié de l’angle
AOB
.
Les angles bleus sont donc tous égaux.
Propriété
Les angles inscrits dans un même cercle qui interceptent le
même arc sont tous égaux.
Remarque : Dans le cas où
[
]
AB
est un diamètre, on retrouve un résultat déjà connu, les angles bleus
mesurent chacun la moitié de
AOB
, soit 90°.

Marc Bizet – collège Pablo Picasso – Harfleur – classe de 3
ème
- 2 -
3. Polygones réguliers
Définition
Un polygone régulier est un polygone inscriptible dans un cercle et dont tous les côtés ont la même
longueur.
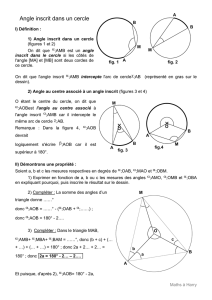
• Déterminer la mesure de
ACB
.
• En déduire la mesure de
AOB
.
• Déterminer la mesure de
AOB
.
• En déduire la mesure de
ADB
.
• Déterminer la mesure de
AOB
.
• En déduire la mesure de
AEB
.
• Déterminer la mesure de
DEB
.