angles inscrits

O
AA1
A2
A3
A4
A5
O
A
O'
M
Chapitre 15 ANGLES INSCRITS
ET POLYGONES RÉGULIERS
I/ Angle inscrit dans un cercle
Définition et vocabulaire :
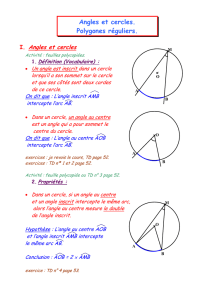
A, M et B sont trois points d’un cercle (C) de centre O.
L’angle ;AOB est un angle au centre qui intercepte l’arc ;AB.
L’angle ;AMB est un angle inscrit qui intercepte l’arc ;AB.
Théorème de l’angle inscrit :
la mesure de l’angle au centre est égale au double de la mesure
de tout angle inscrit qui intercepte le même arc.
Exemple : ;AMB et ;AOB interceptent le même arc ;AB.
O est le centre du cercle donc ;AOB = 2 ;AMB
Conséquence :
Si deux angles inscrits dans un même cercle interceptent le même
arc alors ils ont la même mesure.
II/ Polygones réguliers
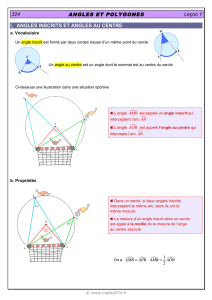
Définition : Un polygone régulier est un polygone inscrit
dans un cercle et dont tous les côtés ont la
même longueur.
Propriétés :
Tous les angles d’un polygone régulier ont la même mesure.
Tous les angles au centre d’un polygone régulier ont la même
mesure.
Construction d’un polygone régulier connaissant son centre et un sommet.
Soit O le centre et A un sommet
On détermine l’angle au centre :  =
Error!
où n est le nombre de côtés du polygone
On construit les sommets par rotations successives de centre O et d’angle .
Exemples :
Pour un pentagone  =
Error!
soit  = 72°.
Pour un hexagone  =
Error!
soit  = 60°.