Cours Angles et Polygones

I)
Angle inscrit et angle au centre
1) Définition:
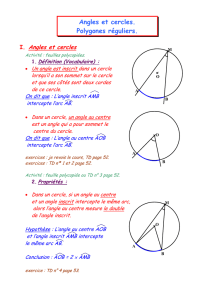
Angle inscrit
Un angle inscrit dans un cercle est un angle dont le sommet est un point
du cercle et dont les côtés coupent le cercle en des points distincts du
sommet. La
partie du cercle compris
s’appelle l’arc intercepté.
2) Définition
: Angle au centre
Un angle au centre est un angle dont le sommet
dont les côtés coupent le cercle en deux points distincts. La partie du
cercle comprise
entre les deux côtés de l’angle
1
ANGLES ET POLYGONES
Angle inscrit et angle au centre
:
Angle inscrit
:
Un angle inscrit dans un cercle est un angle dont le sommet est un point
du cercle et dont les côtés coupent le cercle en des points distincts du
partie du cercle compris
e entre les deux côtés de l’angle
s’appelle l’arc intercepté.
ACB
est un angle
cercle interceptant l’arc AB .
: Angle au centre
:
Un angle au centre est un angle dont le sommet
est
le centre d’un cercle et
dont les côtés coupent le cercle en deux points distincts. La partie du
entre les deux côtés de l’angle
s’appelle l’arc intercepté.
AOB
est un angle au centre
interceptant l’arc AB.
Un angle inscrit dans un cercle est un angle dont le sommet est un point
du cercle et dont les côtés coupent le cercle en des points distincts du
e entre les deux côtés de l’angle
est un angle
inscrit dans le
cercle interceptant l’arc AB .
le centre d’un cercle et
dont les côtés coupent le cercle en deux points distincts. La partie du
s’appelle l’arc intercepté.
est un angle au centre
interceptant l’arc AB.

3) Activité:
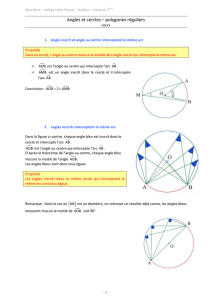
4) Propriété 1:
Si deux angles sont
même arc
alors ils ont la même mesure.
5) Propriété 2:
Si un angle inscrit dans un cercle et un angle au centre relatif à ce cercle
interceptent le même arc alors l’angle au centre mesure le double de
l’angle inscrit.
6) Exemple :
Soit ABD un triangle équilatéral de 4 cm de côté et
circons
crit au triangle ABD. Soit M un point de
même arc que le point D et soit O le centre de
a)
Faire une figure.
b)
Déterminer
2
Si deux angles sont
inscrits dans un même cercle et si ils interceptent le
alors ils ont la même mesure.
AMB
 et ANB
sont deux angles
inscrits dans un même cercle et
interceptant l’arc AB, donc
mesure AMB
=
Si un angle inscrit dans un cercle et un angle au centre relatif à ce cercle
interceptent le même arc alors l’angle au centre mesure le double de
AMB
est un angle inscrit dans
un cercle et
AOB
au centre relatif au même cercle
et ces deux angles interceptent
l’arc AB donc
mesure AOB
= 2×
Soit ABD un triangle équilatéral de 4 cm de côté et
C
le cercle
crit au triangle ABD. Soit M un point de
C
situé sur le
même arc que le point D et soit O le centre de
C.
Faire une figure.
Déterminer
la mesure des angles ADB
 , AMB  et
AOB
inscrits dans un même cercle et si ils interceptent le
sont deux angles
inscrits dans un même cercle et
interceptant l’arc AB, donc
=
mesure ANB
Si un angle inscrit dans un cercle et un angle au centre relatif à ce cercle
interceptent le même arc alors l’angle au centre mesure le double de
est un angle inscrit dans
AOB
est un angle
au centre relatif au même cercle
et ces deux angles interceptent
= 2×
mesure AMB
le cercle
situé sur le
AOB
. Justifier.

Démonstration :
Soien
t trois points A, B et M d’un cercle de
positions,
on peut obtenir
Premier cas :
Deuxième cas :
En conclusion, l
’angle
que celle de l’angle inscrit qui intercepte le même arc. Donc deux angles
inscrits, interceptant le même arc, ont la même m
mesure de l’angle au centre correspondant).
3
t trois points A, B et M d’un cercle de
centre O. Suivants leurs
on peut obtenir
trois cas différents.
Dans le triangle isocèle OAM,
on a
OMA
 MAO
or OMA
MAO
2OMA
 AOM
AOM
De plus,
BOA
 AOM
AOM
D’où
180°  2OMA
Donc 2OMA
D’après le premier cas
AON
 2AMN
NOB
 2NMB
Donc
AON
 NOB
AOB
2
AOB
2
’angle
au centre a donc une mesure deux fois plus grande
que celle de l’angle inscrit qui intercepte le même arc. Donc deux angles
inscrits, interceptant le même arc, ont la même m
esure (la moitié de la
mesure de l’angle au centre correspondant).
centre O. Suivants leurs
Dans le triangle isocèle OAM,
AOM
 180°
MAO
 180°
180°  2OMA
180°
180°  BOA
 180°  BOA
BOA
D’après le premier cas
et
2AMN
 2NMB
2
AMN
 NMB
2
AMB
au centre a donc une mesure deux fois plus grande
que celle de l’angle inscrit qui intercepte le même arc. Donc deux angles
esure (la moitié de la

Troisième cas :
Conclusion identique à celle du premier cas.
II) Polygone régulier :
1) Définition :
Un polygone est régulier lorsque t
tous ses angles ont la même mesure.
Triangle équilatéral
4
D’après le premier cas
NOA
 2NMA
NOB
 2NMB
Donc
NOB
 NOA
AOB
2
AOB
2
Conclusion identique à celle du premier cas.
Un polygone est régulier lorsque t
ous ses côtés ont la même longueur
tous ses angles ont la même mesure.
Triangle équilatéral
Carré
D’après le premier cas
et
2NMB
 2NMA
2
NMB
 NMA
2
AMB
ous ses côtés ont la même longueur
et

5
2) Activité :
3) Propriété :
Un polygone régulier à n côtés est inscriptible dans un cercle. Tous les
angles au centre relatifs à ce cercle et déterminés par deux sommets
consécutifs du polygone, ont la même mesure :
°
 .
4) Exemple :
a) Construire un triangle équilatéral ABC de centre O tel que
OA = 2,5 cm.
b) Construire un carré ABCD de centre O tel que OB = 3,5 cm.
c) Construire un hexagone régulier ABCDEF de centre O tel que
OC = 4 cm.
d) Construire un octogone régulier ABCDEFGH de 3 cm de côté.
Justifier.