R.Flouret Exercice 1 : En considérant la figure ci

R.Flouret
Exercice 1 :
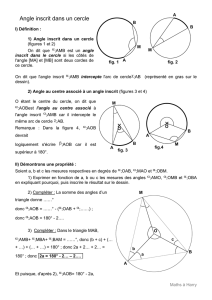
En considérant la figure ci-après, calculer les mesures des angles du triangle ABC.

R.Flouret
Exercice 2 :
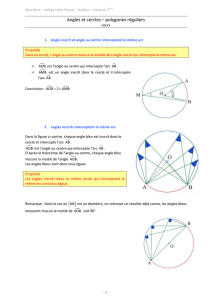
Prouver dans les 2 cas que
AMB
=
C
N
D
1
er
cas : O est le centre du cercle
2
ième
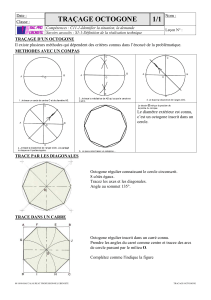
cas : M et N sont les centres des cercles

R.Flouret
Exercice 3 : (Brevet National 2010)
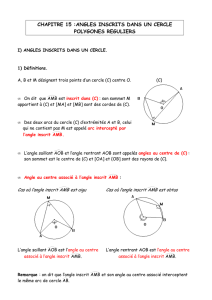
On considère la figure ci-dessous :
MNOP est un carré de côté 9 cm.
1) Calculer .AH
2) L’octogone ABCDEFGH est-il un octogone régulier ? Justifier la réponse.
3) Calculer l’aire de l’octogone ABCDEFGH.
4) Soit S le point d’intersection des diagonales du carré MNOP.
Le disque de centre S et de diamètre 9 cm a-t-il une aire supérieure à l’aire de l’octogone ?

R.Flouret
Corrigé 1 :
A
O
B
est l’angle au centre associé à l’angle inscrit
A
C
B
.
D’après le théorème de l’angle inscrit, on en déduit que
A
C
B
2
1
=
A
O
B
Or
A
O
B
°
=
85
Donc
A
C
B
85
2
1×=
A
C
B
°
=
5,42
Les angles
B
A
C
et
B
M
C
interceptent le même arc donc
B
A
C
=
B
M
C
Or
B
M
C
= 32°
Donc
B
A
C
°
=
32
La somme des mesures des angles d’un triangle est égale à 180 °
Donc
A
C
B
+
B
A
C
+
ABC
= 180 °
ABC
= 180° - (
A
C
B
+
B
A
C
)
ABC
= 180° - (42,5+32)
ABC
= 105,5°
Corrigé 2 :
1
er
cas :
C
OD
est l’angle au centre associé à l’angle inscrit
C
N
D
.
D’après le théorème de l’angle inscrit, on a
C
N
D
2
1
=
C
OD
Les angles
C
OD
et
AO
B
sont opposés par le sommet donc
C
OD
=
AO
B
L’angle
AO
B
est l’angle au centre associé à l’angle inscrit
A
M
B
.
D’après le théorème de l’angle inscrit, on a
A
M
B
2
1
=
AO
B
Or
C
OD
=
AO
B
Donc
2
1
C
OD
2
1
=
AO
B
c’est-à-dire
C
N
D
=
AMB

R.Flouret
2
ième
cas :
C
N
D
est l’angle au centre associé à l’angle inscrit
C
ID
.
D’après le théorème de l’angle inscrit, on en déduit que
C
ID
2
1
=
C
N
D
Les angles
C
ID
et
AIB
sont opposés par le sommet donc
C
ID
=
AIB
A
M
B
est l’angle au centre associé à l’angle inscrit
AIB
.
D’après le théorème de l’angle inscrit, on en déduit que
AIB
2
1
=
A
M
B
Or
C
ID
=
AIB
Donc
2
1
C
N
D
2
1
=
A
M
B
c’est-à-dire
C
N
D
=
A
M
B
.
Corrigé 3 :
1) MNOP est un carré donc MAH est un triangle rectangle en M.
On a cm
MN
MHMA 3
3
9
3
====
MAH est un triangle rectangle en M.
D’après le théorème de Pythagore, on a :
cmAH
AH
AH
AH
AH
AH
AH
MAMHAH
23
29
29
18
18
99
33
2
2
222
222
=
=
×=
=
=+= += +=
2) Le polygone ABCDEFGH n’est pas un polygone régulier car tous ses côtés n’ont pas la même longueur.
En effet, on a par exemple
AB
AH
≠
.
3) Les triangles PGF, MAH, BNC et DOE sont clairement superposables. Ils ont donc la même aire.
Soit
A’ l’aire du carré MNOP et A l’aire du polygone ABCDEFGH.