Angles et cercles. Polygones réguliers. I. Angles et cercles

Angles et cercles.
Polygones réguliers.
I. Angles et cercles
Activité : feuilles polycopiées.
1. Définition (Vocabulaire) :
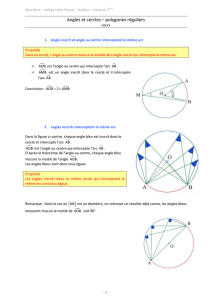
• Un angle est inscrit dans un cercle
lorsqu’il a son sommet sur le cercle
et que ses côtés sont deux cordes
de ce cercle.
On dit que : L’angle inscrit AMB
intercepte l’arc AB.
• Dans un cercle, un angle au centre
est un angle qui a pour sommet le
centre du cercle.
On dit que : L’angle au centre AOB
intercepte l’arc AB.
exercices : je revois le cours, TD page 52.
exercices : TD n°
s
1 et 2 page 52.
Activité : feuille polycopiée ou TD n° 3 page 52.
2. Propriétés :
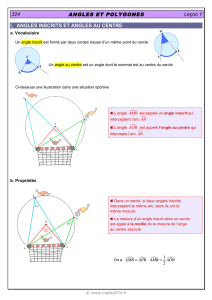
• Dans un cercle, si un angle au centre
et un angle inscrit intercepte le même arc,
alors l’angle au centre mesure le double
de l’angle inscrit.
Hypothèse : L’angle au centre AOB
et l’angle inscrit AMB intercepte
le même arc AB.
Conclusion : AOB = 2 × AMB
exercice : TD n° 4 page 53.
A
B
M
O
A
B
O
A
B
M
O

• Dans un cercle, si deux angles inscrits interceptent le même arc,
alors ils ont la même mesure.
Hypothèse : Les angles inscrits AMB
et ANB interceptent le même arc AB.
Conclusion : AMB = ANB
exercices : je revois le cours, TD page 53.
exercices : TD n° 5 page 53.
Remarques :
Dans le cas où [AB] est un diamètre,
on retrouve un résultat déjà connu :
AMB = ANB = AOB : 2
= 180 : 2
= 90°
d’où : AMB triangle rectangle en M.
Rappelez-vous : « Si on joint un point du cercle
aux deux extrémités d’un diamètre donné, alors on obtient un triangle
rectangle ».
ANB angle inscrit associé à l’angle au centre AOB.
Ils interceptent le même arc AB (« le grand »).
donc : ANB =
1
2
AOB
AB
O
N
AB
M
O
N
A
B
M
O
N

II. Polygones réguliers.
1. Définition :
Un polygone est dit « régulier » quand :
- Tous ses côtés ont la même longueur.
- Tous ses angles ont la même mesure.
Exemple :
Un triangle équilatéral et un carré sont des polygones
réguliers.
2. Cercle circonscrit :
Dans un polygone régulier, il existe un cercle de centre O qui
passe par tous les sommets.
On appelle ce cercle le cercle circonscrit au polygone.
Le point O est appelé centre du polygone.
Propriété :
Dans un polygone régulier, tous les angles au centre sont
égaux.
Conséquence :
Deux sommets consécutifs sont images par une rotation de
centre O et d’angle (360/n), où n est le nombre de côtés du polygone.
Exemples :
Triangle équilatéral
n = 3
α =
360
3 = 120°
Carré
n = 4
α =
360
4 = 90°
Hexagone régulier
n = 6
α =
360
6 = 60°
exercices : TD n°
s
6, 7 et 8 page 54.
AB
A
C
O
B
O
F
O
C
D
A
B
D
E
C
60°
90°
120°