CH04 - Fiche d`exercices - Tivomaths

Premi` ere S Novembre 2015
CH04 - Fiche d’exercices
Th` eme : D´ erivation.
I Nombre d´eriv´e
Exercice 1.
Soient f,get hles fonctions d´efinies sur Rpar :
f(x) = −x+ 1 , g(x) = x2−xet h(x) = −x2+ 2x
1. V´erifier que fest d´erivable en 1et calculer son
nombre d´eriv´e en 1.
2. Mˆeme question pour get hen −1.
Exercice 2.
Soit ila fonction inverse d´efinie sur R∗par i(x) = 1
x.
Montrer que iest d´erivable en −3et calculer i′(−3).
Exercice 3 (Fonction affine).
1. D´eterminer le nombre d´eriv´e de la fonction
f:x7→ 2x−3en a= 3 et a=−6.
2. Que peut-on conjecturer ?
3. D´eterminer f′(a)pour un r´eel aquelconque.
Exercice 4 (Fonction constante (T)).
Soit kun r´eel fix´e.
1. D´eterminer le nombre d´eriv´e de la fonction
f:x7→ ken a= 3 et a=−6.
2. Que peut-on conjecturer ?
3. D´eterminer f′(a)pour un r´eel aquelconque.
Exercice 5.
1. Soit f:x∈R7→ −2x2+ 3x+ 2.
Montrer que fest d´erivable en 2et calculer f′(2).
2. Soit g:x∈R\ {−5} 7→ 2x−1
x+ 5 .
Montrer que gest d´erivable en 2et calculer g′(2).
Exercice 6 (AP).
Soit f:x∈R+7→ √x3+ 2x+ 1.
Voici un algorithme incomplet, ´ecrit avec AlgoBox.
1. Compl´eter cet algorithme afin qu’il renvoie les va-
leurs successives du quotient f(a+h)−f(a)
h, pour
des valeurs de h´egales `a 10−n, o`u nd´ecrit les entiers
naturels entre 2et 10.
2. Tester cet algorithme (sur AlgoBox ou calculatrice)
et conjecturer f′(1) puis f′(8).
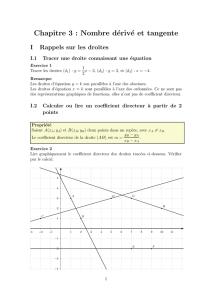
II Tangente & nombre d´eriv´e
Exercice 7.
On a repr´esent´e la courbe d’une fonction fet certaines
de ses tangentes.
1. a) Rappeler l’interpr´etation graphique de f′(3).
b) Lire graphiquement f′(3).
2. De mˆeme, lire f′(−5),f′(−3) et f′(0).
Exercice 8.
On consid`ere une fonction gadmettant la repr´esentation
graphique ci-dessous.
Par lecture graphique, d´eterminer le signe de :
g′(−3) ; g′(−1) ; g′(0) ; g′Å1
2ã
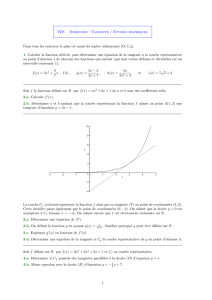
Exercice 9.
Soit fla fonction d´efinie sur Rpar f(x) = −x2+ 4x.
1. Montrer que fest d´erivable en 1et calculer f′(1).
2. D´eterminer une ´equation de la tangente T`a la
courbe C
fde fau point d’abscisse 1.
Exercice 10.
Soit fune fonction de courbe C
fadmettant en son point
Ad’abscisse −1une tangente d:y= 2x+ 3.
Calculer f(−1) et f′(−1).
Exercice 11.
On reprend la fonction inverse ide l’exercice 2.
D´eterminer l’´equation r´eduite de la tangente `a la courbe
de iau point d’abscisse −3.
Corrig´e disponible sur http://tivomaths.free.fr/ - 1/3-L
A
T
E
X 2ε

Exercice 12.
Voici une capture d’´ecran du logiciel de calcul formel
Xcas:
Utiliser les r´esultats du logiciel pour r´epondre aux ques-
tions suivantes.
1. Donner une ´equation de la tangente T`a la courbe C
de la fonction fen son point d’abscisse 2
3.
2. ´ Etudier la position de Cpar rapport `a T.
3. Contrˆoler graphiquement sur la calculatrice.
Exercice 13. (T)
Dans un rep`ere orthonorm´e d’origine O,Cest le demi-
cercle de centre Oet de rayon 1repr´esent´e sur la figure
suivante.
1. Justifier que Cest la courbe repr´esentative de la
fonction f:x∈[−1 ; 1 ] 7→ √1−x2.
2. On ´etudie la d´erivabilit´e de fen 1
2.
a) Expliquer les calculs suivants r´ealis´es par le logi-
ciel de calcul formel Xcas:
b) On admet les r´esultats du logiciel. Quelle est la
valeur de f′Å1
2ã?
3. a) D´eterminer une ´equation de la tangente T`a C
en A.
b) Prouver que (OA)⊥T.
4. Que met en ´evidence cet exercice ?
Exercice 14 (AP).
Voici un programme ´ecrit sur calculatrice, sachant que
l’utilisateur a, au pr´ealable, entr´e une fonction dans Y1.
Que repr´esentent les valeurs
de sortie de ce programme ?
Expliquer.
III D´eriv´ee d’une fonction
Exercice 15.
Calculer f′(a)pour :
1. f(x) = x2et a=−5
2. f(x) = x4et a=−3
3. f(x) = √xet a= 4
4. f(x) = 1
xet a= 3
Exercice 16.
On consid`ere la courbe Cd’´equation y=√x.
1. D´eterminer une ´equation de la tangente `a Cen son
point d’abscisse 4.
2. La droite ∆, de cœfficient directeur 1
6, est une tan-
gente `a Cen un point A.
D´eterminer les coordonn´ees de Aet pr´eciser l’´equa-
tion r´eduite de ∆.
Exercice 17 (Calculs de fonctions d´eriv´ees).
Calculer la d´eriv´ee de la fonction fdans chacun des cas
suivants :
1. Somme
a) f(x) = x2+ 5
b) f(x) = x2+√x+ 4
c) f(x) = x4+x3+x5
d) f(x) = √x+1
x
2. Produit par un r´eel
a) f(x) = 4x
b) f(x) = 6x2
c) f(x) = −5x3
d) f(x) = 12√x
e) f(x) = −6
x
3. Produit par un r´eel et somme
a) f(x) = −2x5+ 3x−1
4x2−1 3
b) f(x) = −x3+x2√2 + 4x
c) f(x) = 8√x−4x
d) f(x) = 4x−1
3
e) f(x) = x4+ 3x2−5x
4
f) f(x) = 2
x−2x+ 3√x
Corrig´e disponible sur http://tivomaths.free.fr/ - 2/3-L
A
T
E
X 2ε

4. Produit de deux fonctions
a) f(x) = x√x
b) f(x) = 4x(x−5)
c) f(x) = x3(x−√x)
d) f(x) = (3x+ 4)(x2−5)
e) f(x) = 1
x(3 + √x)
5. Inverse
a) f(x) = 1
x2−1
b) f(x) = 2
x+ 4
c) f(x) = −5
1 + x2
6. Quotient
a) f(x) = 2x2
x+ 3
b) f(x) = 2x2+ 5x+ 1
x2+ 1
c) f(x) = 2√x+ 3
x
7. En vrac. . .
a) f(x) = 2x+ 3
x−5
b) f(x) = (2 −x)√x
c) f(x) = (2√x+ 1) x2
d) f(x) = x√x
x−2
e) (T) f(x) = 2x2−5x+ 1
f) (T) f(x) = 1
x2−4
g) (T) f(x) = 4
x4+ 1
h) (T) f(x) = x√x+2x−1
x+ 1
i) (T) f(x) = (x2−1)(3x3−2x2+ 1)
Exercice 18 (Logique).
La phrase «si f(x) = x2+ 10, alors f′(x) = 2x»est
une implication vraie.
1. ´ Enoncer l’implication r´eciproque.
2. Cette implication r´eciproque est-elle vraie ? Justifier.
Exercice 19.
Soit fla fonction d´efinie sur Rpar f(x) = x3−3x2+ 3
et de courbe C
f.
1. Montrer que fest d´erivable sur Ret calculer f′(x)
pour tout x∈R.
2. D´eterminer l’´equation r´eduite de ∆, la tangente `a C
f
au point d’abscisse 1.
3. D´eterminer les abscisses des points de C
fen lesquels
la tangente `a C
fest parall`ele `a la droite d’´equation
r´eduite y= 9x+ 2.
4. D´eterminer les abscisses des points de C
fen lesquels
la tangente passe par B(1; 3).
Corrig´e disponible sur http://tivomaths.free.fr/ - 3/3-L
A
T
E
X 2ε