Dans chaque cas, f est une fonction définie et dérivable sur un

Lycée Camille SEE
20 Mars 2009 CONTRÔLE N°7 1re ES Durée 1 heure
EXERCICE 1
Dans chaque cas, fest une fonction définie et dérivable sur un intervalle I. Calculer f′(x).
1. fest définie sur ]0;+∞[ par f(x)=x3
2−3x2+5 x
2. fest définie sur ]1;+∞[ par f(x)=√x
x−1.
3. fest définie sur Rpar f(x)=(1−2x)0,5x2+1
EXERCICE 2
Donner une équation de la tangente à la parabole d’équation y=x2−3x+5 au point d’abscisse −1.
EXERCICE 3
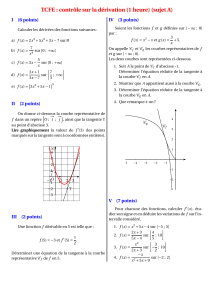
Sur la figure ci-dessous, Cfest la courbe représentative d’une fonction fdérivable sur R. Les droites d1,d2,d3
et d4sont tangentes à la courbe Cf.
1
2
3
4
5
6
7
-1
-2
-3
-4
1 2 3 4 5 6-1-2-3-4-5-6-7-8 0x
y
d1
d2
d3
d4
Cf
B
A
1. Déterminer graphiquement f(−4), f(−2) et f(2).
2. Déterminer graphiquement les nombres dérivés f′(−4) et f′(2).
3. La tangente à la courbe Cfau point Ad’abscisse −2 passe par l’origine du repère. Déterminer f′(−2).
4. La tangente Tà la courbe Cfau point B −6; 8
3!est parallèle à la droite d4. Déterminer f′(−6) puis, donner
une équation de la tangente Tà la courbe au point B. Tracer cette droite sur le graphique précédent.
EXERCICE 4
Soit fla fonction définie sur Rpar f(x)=5x+3
x2−x+1. On note f′sa fonction dérivée.
1. Calculer f′(x) .
2. a. Étudier le signe de f′(x) .
b. En déduire le tableau des variations de la fonction f. (Indiquer dans le tableau de variation, les valeurs
exactes des extremum).
MATH@ES