Tangente / Études graphiques. Dans tous les exercices le plan est

TES Exercices : Tangente / ´ Etudes graphiques.
Dans tous les exercices le plan est muni du rep`ere orthonorm´e (O,~ı,~,).
1. Calculer la fonction d´eriv´ee, puis d´eterminer une ´equation de la tangente `a la courbe repr´esentative
au point d’abscisse 1 de chacune des fonctions qui suivent (qui sont toutes d´efinies et d´erivables sur un
intervalle contenant 1),
f(x) = 5x2+8
7x−115, g(x) = 3x−5 2x+ 7, h(x) = 5x 2x2+ 3 et i(x) = 7√x+ 3.
Soit fla fonction d´efinie sur Rpar f(x) = ax2+bx + 1 o`u aet bsont des coefficients r´eels.
2.a. Calculer f0(x).
2.b. D´eterminer aet bsachant que la courbe repr´esentant la fonction fadmet au point A(1,2) une
tangente d’´equation y= 3x−1.
La courbe Cfci-dessus repr´esente la fonction fainsi que sa tangente (T) au point de coordonn´ees (3,2).
Cette derni`ere passe ´egalement par le point de coordonn´ees (0,−4). On admet que la droite y= 0 est
asymptote `a Cflorsque x→ −∞. On admet encore que fest strictement croissante sur R.
3.a. D´eterminer une ´equation de (T).
3.b. On d´efinit la fonction gen posant g(x) = 1
f(x). Justifier pourquoi gpeut ˆetre d´efinie sur R.
3.c. Exprimer g0(x) en fonction de f0(x).
3.d. D´eterminer une ´equation de la tangente `a Cgla courbe repr´esentative de gau point d’abscisse 3.
Soit fd´efinie sur Rpar f(x) = 3x3+ 3x2+ 2x+ 1 et Cfsa courbe repr´esentative.
4.a. D´eterminer si Cfposs`ede des tangentes parall`eles `a la droite (D) d’´equation y=x.
4.b. Mˆeme question avec la droite (E) d’´equation y=−5
4x+ 7.
1

Soient a,b,cet ddes nombres r´eels. On consid`ere la fonction fd´efinie sur Rpar f(x) = ax3+bx2+cx+d
dont la courbe repr´esentative Cfdans le plan muni du rep`ere (O,~ı, ~) est donn´ee ci-dessous. (T) est la
tangente `a Cfau point Aet (S) est la tangente `a Cfau point C. Les points A,Bet Cont respectivement
pour coordonn´ees (−2,3), ¡−3
2,7¢et (0,−5).
5.a. D´eriver f(x) et trouver l’expression de f0(x) en fonction de x,a,b,cet d.
5.b. D´eterminer les valeurs de f(−2), f0(−2), f(0) et f0(0).
5.c. ´ Ecrire un syst`eme de quatre ´equations d’inconnues a,b,cet d`a partir des r´esultats pr´ec´edents.
5.d. R´esoudre le syst`eme de quatre ´equations trouv´e `a la question pr´ec´edente et en d´eduire quelles sont
les valeurs de a,b,cet d.
5.e. D’apr`es le graphique Cfadmet une tangente (U) parall`ele (et non confondue) `a (T). D´eterminer
par le calcul une ´equation de (U).
2

Soient a,b,cet ddes nombres r´eels. On consid`ere la fonction gd´efinie sur R\ {−d
c}par
g(x) = ax +b
cx +d
dont la courbe repr´esentative Cgdans le plan muni du rep`ere (O,~ı,~) est donn´ee ci-dessous. (T) est la
tangente `a Cgau point Bd’abscisse 3 et (S) est la tangente `a Cgau point Ad’abscisse 1. Cgadmet
la droite (Γ) : y=3
2comme asymptote horizontale aussi bien lorsque x→ −∞ que lorsque x→+∞.
Cgadmet la droite (∆) : x=3
2comme asymptote verticale. C¡3 2,31 6¢est le point d’intersection entre
(T) et (∆), D(0,7) est le point d’intersection entre (S) et (T), E¡7
11 ,0¢est le point d’intersection entre
l’axe des abscisses et (S).
6.a. D´eriver g(x) et trouver l’expression de g0(x) en fonction de x,a,b,cet d.
6.b. D´eterminer en s’appuyant sur le graphique les valeurs de g0(1) et g0(3). On se servira des points
dont les valeurs exactes des coordonn´ees sont donn´ees dans l’´enonc´e.
6.c. Trouver deux ´equations d’inconnues a,b,cet d`a partir des deux valeurs pr´ec´edentes.
6.d. D´eterminer une troisi`eme ´equation d’inconnues aet cen utilisant l’asymptote (Γ).
6.e. D´eterminer une quatri`eme ´equation d’inconnues cet den utilisant l’asymptote (∆).
6.f. On admet que c= 2. Terminer la r´esolution du syst`eme de quatre ´equations trouv´e `a la question
pr´ec´edente et en d´eduire quelles sont les valeurs de a,b,cet det quelle est l’expression explicite de
g(x).
6.g. Calculer g(1) et g(3).
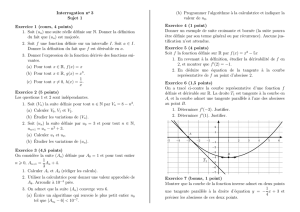
Le graphique ci-dessus est celui de Cula courbe repr´esentative de la fonction ud´efinie sur l’intervalle
[−5,5]. Les points Aet Bont respectivement pour coordonn´ees (1,1) et (3,0). (T) est la tangente `a
Cuau point A.
7.a. D´eterminer u0(1) puis une ´equation de (T).
7.b. On d´efinit une seconde fonction fen posant f=v◦uo`u vd´esigne la fonction racine carr´ee.
Justifier pourquoi fest correctement d´efinie sur l’intervalle [−5,5].
7.c. Calculer f0(1) et f(1).
3