1 STI2D1 lundi 10 f´evrier
Devoir de math´ematiques no5
La qualit´e de la r´edaction, la clart´e et la pr´esentation des raisonnements entreront pour une part importante dans
la notation.
L’usage de la calculatrice est autoris´e.
Exercice 1 : (8 points)
Calculer la fonction d´eriv´ee de chacune des fonctions suivantes, d´efinies et d´erivables sur I.
a) f(x) = 8√x I =R∗+;
b) g(x) = x7+1
x+1
x5I=]0; +∞[;
c) h(x) = 4x3−5x2+ 7x−8I=R;
d) k(x) = (x2+ 1) (3x−5) I=R;
e) ϕ(x) = 3x2−5x+ 2
x+ 1 I=] − ∞;−1[.
1
2
3
4
5
−1
−2
−3
−4
−5
−6
1 2 3 4 5−1−2−3−4
××
#”
i
#”
j
O
Cf
T1
T2
A
B
Exercice 2 : (4 points)
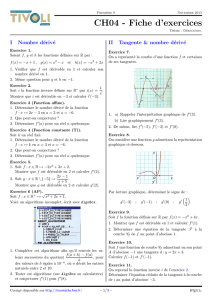
Soit fune fonction d´efinie sur Rdont la repr´esentation gra-
phique Cfest r´epr´esent´ee dans le rep`ere (O;#”
ı ,#”
)ci-contre.
Les droites T1et T2sont tangentes au point A(3 ; −3) et
au point B(0 ; −3) `a la courbe Cf.
1) a) En utilisant les donn´ees du graphique, d´eterminer les
coefficients directeurs respectifs des tangentes T1et T2.
b) En d´eduire les nombres d´eriv´es f′(3) et f′(0).
2) On admet l’´egalit´e f′(1) = 0. Que peut-on en d´eduire
pour la tangente au point d’abscisse 1`a la courbe Cf?
Exercice 3 : (5 points)
On consid`ere la fonction polynˆome d´efinie sur Rpar :
f(x) = −x2+x+ 1.
1) Calculer f′(x)pour tout x∈R.
2) Donner une ´equation de la tangente au point d’abscisse 2`a la courbe repr´esentative de f.
3) D´eterminer l’abscisse du point de la courbe repr´esentative de f, o`u la tangente a pour coefficient
directeur −4.
Exercice 4 : (3 points)
Soit fla fonction d´efinie pour tout r´eel xpar f(x) = x2+bx + 5, o`u best une constante r´eelle.
Dans cet exercice, on veut d´eterminer la valeur de b.
Sachant que la tangente `a la courbe repr´esentative de fau point d’abscisse 1est parall`ele `a la droite ∆
d’´equation y= 3x+√2, calculer la valeur de b.
http://mathematiques.ac.free.fr
1
/
1
100%