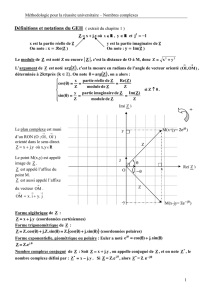
Carré du nombre i Forme algébrique d`un nombre complexe Forme

Carré du nombre i
On définit le nombre i de la façon
suivante. i=−1
Forme algébrique d'un nombre complexe
Tout nombre complexe z peut s'écrire
sous une forme algébrique.
z=a+ib
Re(z) = a (partie réelle de z)
Im(z) = b (partie imaginaire de z)
Forme trigonométrique, module et argument d'un nombre complexe
Tout nombre complexe z peut s'écrire
sous une forme trigonométrique.
z=r(cos(θ) + isin(θ)
r est le module de z.
θ est un argument de z.
Notation exponentielle
Un nombre complexe z, de module r et
d'argument θ a la forme exponentielle
suivante :
re
Relations entre forme trigonométrique et forme algébrique
Si z admet la forme trigonométrique
z=r(cos(θ) + isin(θ)), alors :
Re(z) = rcos(θ)
Im(z) = rsin(θ)
!FORMULES ET THÉORÈMES
2
!
iθ
!

Définition du conjugué
Soit z=a+ib, où a et b sont des réels.
On appelle le conjugué de z.=a−ib
z=a+b
Propriétés du conjugué
Soient z et z deux nombres complexes. = +
=×
=, si z≠0
Définition du module
Soit z=a+ib, où a et b sont des réels.
On note ∣z∣ le module de z.∣z∣=
Propriétés du module
Soient z et z deux nombres complexes,
et n un entier naturel. ∣z∣=
∣z∣=∣z∣
∣zz ∣=∣z∣∣z∣
∣ ∣ =, si z n'est pas nul
∣z+z∣ ≤ ∣z∣+∣z∣
Argument d'un nombre complexe
z¯!z¯!
z¯!2 !2 !
′
z+z′
!! z¯!z′ !
¯
!
z×z′
!! z¯!z′ !
¯
!
(z′
!
z
!) !
z′
!
¯
!
z¯!!′
!
√a+b
2
!2 !!
′
√zz¯!!
n
!n !
′
!′ !
z′
!
z
!
∣z∣
′
!
∣z∣
!′ !
′
!′ !

Soit z un nombre complexe non nul et M
le point du plan dont il est l'affixe. arg(z) = ( ; ).
Argument et opérations
Soient z et z deux nombres complexes,
et n un entier naturel. arg(z) = narg(z)
arg(zz ) = arg(z) + arg(z)
arg( ) = arg(z)−arg(z)
arg(−z) = arg(z) + π
arg( ) = −arg(z)
Définition de l'affixe d'un point
Soit M un point de coordonnées (x;y)
dans le plan muni du repère orthonormé
(O; , ).
On note z son affixe, définie comme
suit.
z=x+iy
Définition de l'affixe d'un vecteur
Soit un vecteur du plan de
coordonnées (x,y).
On note z son affixe, définie comme
suit.
z=x+iy
Calcul de la longueur d'un segment à l'aide des affixes
Soient A et B deux points du plan.
On note z et z leurs affixes
respectives.
AB =∣z−z∣
u!OM!
′n
!
′
!′ !
z′
!
z
!′ !
z¯!
u!v!
M
M
!
w!
w
w!!
A B A
!B !

Calcul d'un angle orienté à l'aide des affixes
Soient A, B, C et D des points distincts
du plan.
On note z, z, z et z leurs affixes
respectives.
( , ) = arg( )
Affixe d'un vecteur
Soient A et B deux points du plan.
On note z et z leurs affixes
respectives.
On note z l'affixe du vecteur ,
définie comme suit.
z=z−z
Résolution dans C d'une équation du second degré avec Δ< 0
Soit (E) : ax +bx +c= 0 une
équation du second degré de discriminant
Δ< 0.
(E) admet 2 solutions distinctes
complexes x et x.
x=
x=
A B C D
AB!CD!
z−z
B
!A !
z−z
D
!C !
!
A B
AB!AB!
AB!!B
!A !
2
1 2
1
!2a
−b−i√−Δ!
!
2
!2a
−b+i√−Δ!
!

Les nombres complexes
A
Propriété
!
Nombre i
Il existe un nombre noté i vérifiant :
i=−1
Propriété
!
Ensemble des nombres complexes
Il existe un ensemble de nombres, noté C, qui contient R et i.
On l'appelle ensemble des nombres complexes.
Propriété
1FORME ALGÉBRIQUE
Nombres complexes et forme algébrique
2