Les nombres complexes

Les nombres
complexes
I. Définition
Un nombre complexe z s’écrit sous la forme z = a+ b
⋅
i (ou a+b
⋅
j) où a
et b sont des nombres réels et où i (ou j) est un nombre complexe
qui vérifie i
2
= -1 (ou j
2
= -1).
N.B. i étant aussi la lettre qui représente l’intensité, on peut utiliser la
lettre j pour ne pas les confondre.
Cette écriture est appelée écriture algébrique d’un nombre complexe.
a est appelée partie réelle de z et b, partie imaginaire de z.
L’ensemble des nombres complexes est noté !.
Exemples : 2 + 3 i ; 3i ; 5 ; 0. En prenant b = 0, on remarque qu’un
nombre réel est en particulier un nombre complexe. ( ⊂!!
).
II. Opérations
Soit z = a+bi ; z’ = a’+b’i, deux nombres complexes (a, b, a’ et b’ réels)
! Egalité de complexes
Deux nombres complexes sont égaux si et seulement si leurs parties
réelle et imaginaire sont égales. z = z’ ⇔ a = a’ et b = b’.
En particulier : z = 0 ⇔ a = 0 et b = 0.
! Somme
z + z’ = (a+a’) + (b+b’) i
(a+a’ est la partie réelle de z+z’ et b+b’, sa partie imaginaire)
Exemple : (3 – i) + (1 + 2i ) = 2 + ( 2-1) i.
! Produit
z
× z’ = (a
⋅
a’ - b
⋅
b’) + (a
⋅
b’+a’
⋅
b) i
La formule utilise, en particulier, que i
2
= -1.
Exemple : (3 – i)
× (1 + 2i) = 3 (1 + 2i) – i (1 + 2i)
= 3 + 3 2i - i - 2i
2
= (3+ 2)+ (3 2 -1) i.
! Conjugué
Le complexe conjugué de z, est = a – b
⋅
i.
Exemple : = 2 – 5 i.
! Inverse
L’inverse de z, non nul, est 1
z=
22
a
a+b -
22
b
a+b i.
Exemple : 1
25i+= 25 (2 5 )(2 5 )
i
ii
−
+−
=
22
25
2(5)
i
i
−
− = 2 29 - 5 29 i.
On a multiplié numérateur et dénominateur par le nombre complexe
conjugué et utilisé une identité remarquable (valables aussi dans !).
! D’autres propriétés :
= z = =
z × = a2 + b2 = =
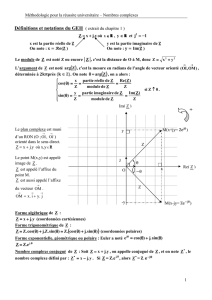
III. Représentation géométrique
Dans un repère orthonormal (O ;
i
"
;
j
"
), au nombre complexe z = a+bi,
on associe son image, le point M (a ; b).
Inversement, on dit qu’un point M(a ; b) a pour affixe z = a +bi.
En terme de vecteur, l’image du nombre complexe z = a+bi est le
vecteur
uOM=
" ####"
(a ; b) et l’affixe du vecteur
uOM=
"####"
(a ; b) est z = a+bi.
Définition :
Soit z = a+ bi d’image M(a ; b).
On définit le module de z : |z| = OM =
22
a+b (=
×zz
et noté )
On définit un argument de z (non nul) : arg (z) = (
i
"
;
OM
####"
) à 2 près.
On appellera Argument de z (noté ) la valeur appartenant à [0 ; 2 [.
Propriétés :
• | | = | z | et arg ( ) = - arg(z).
• Soit A (zA) et B (zB), on a : AB = |zB - zA| et
arg (zB - zA) = (
i
"
; AB
###"
) à 2 près.
Ecriture trigonométrique
Un nombre complexe z aura une écriture unique de la forme [ ].
On appellera cette écriture, écriture trigonométrique de z.
z = [ ] = ( cos )+ i ( sin )
IV. Forme algébrique-Forme trigonométrique
! Forme algébrique vers trigonométrique
Soit z un nombre complexe de forme algébrique z = a+bi.
On veut écrire z sous la forme trigonométrique :
z = [ ] = ( cos )+ i ( sin )
On a : =
22
a+b et z
ρ
=
22
a
a+b
+
22
b
a+b
i = cos + i sin , donc :
ρ
θθ θ
!=
"
#==
"
$
22
22 22
a+b
ab
tel que : cos et sin
a+b a+b
! Forme trigonométrique vers algébrique
Soit z un nombre complexe de forme trigonométrique z = [ ].
On veut écrire z sous la forme algébrique.
On a z = [ ] = ( cos ) + i ( sin ), donc on pose :
ρ θ
ρ θ
=
!
#=
$
a cos
b sin
et on a z = a+bi où a et b sont des nombres réels.
V. Exemple de calculs (Bac STI, 09/2008)
Enoncé : Dans le plan complexe , on considère les points A et B
d’affixes respectives zA = 3 + i 3 et zB = 3 – i 3.
Question : Déterminer le module et un argument de chacun des
nombres complexes zA et zB.
Réponse :
|zA|= |3 + i 3|=
3) 3 12 2 3===
22
3+( 9+
.
23
z
=
3
23
+3
23
i =
3
2
+1
2i = cos + i sin .
On cherche qui vérifie cos =
3
2
et sin = 1
2. =
π
6 convient.
On a donc zA = [ 23;
π
6 ]. Remarquons que zB = , on a donc :
|zB|=| |=|zA|= 23 et arg zB = - arg zA=
π
−6. zB = [ 23 ; -
π
6 ].
Editeur : MemoPage.com SA © / Auteur : Pierre Larivière. / 2008