Les polynômes

Les polynômes
Expressions algébriques
Cas particulier : les polynômes
Un polynôme est une expression rationnelle en x, qui peut être établie à partir de la
lettre x et de constantes quelconques, au moyen des seules opérations d’addition, de
soustraction et de multiplication ( la division étant exceptée ).
Par exemple : x
2 x2 – 7
! ! 1/x n’est pas un polynôme ! !
Les facteurs constants de chaque terme sont appelés coefficients
Le degré d’un polynôme est l’exposant le plus élevé des puissances de x, lorsque
les opérations indiquées ont été poursuivies aussi loin que possible
Exemples : x2 + 3x + 2 est de degré 2
( x + 3 ) ( x + 5 ) – x2 est de degré 1
Il existe également des polynômes à variables multiples.
Exemples : 3 x2 y3 + 4 x2 y – 3 y + x – 7
(x–y)(y+z)
RAPPEL : notion d’identité
Si une relation d’égalité est vérifiée pour toute valeur de x pour laquelle chacune des
expressions qu’elle comporte a une valeur, on appelle identité cette relation d’égalité.
Exemple : ( x + 1 )2 = x2 + 2x + 1
Cela est vérifié quel que soit x.
Par contre : soit l’égalité 2x + 3 = x + 6
Il ne s’agit pas là d’une identité car pour x =1 elle donne 5 = 7 ce qui
est Faux !
Egalité
Calculer a ,b, c sachant que P et Q sont égaux :
P:3x+2
Q : a x + b(x + 1)
Q : a x +b x +b
Q : (a + b) x + b
D’ou a + b = 3 et b = 2
Et donc a + 2 = 3
D’ou a = 1
Calcul d’une valeur numérique
Ex : Calculer la valeur numérique pour x=-2 de
-5x3 + 7x2 + 4x – 5
Il suffit de remplacer x par –2 dans le polynôme et de calculer l’expression ainsi
trouvée
Dans ce cas :
-5 (-2)3 + 7 (-2)2 + 4 (-2) – 5 =40 + 28 – 8 – 5 = 55
Ex : Calculer le nombre réel a de telle manière que la valeur numérique de
4 x2 – (2a – 1)x + 3a pour x = 3 soit 2
solution :
4 . 32 – (2a – 1) . 3 + 3a = 2
36 – 6a + 3 + 3a = 2
d’ou 36 – 6a + 3 + 3a = 2 et - 3a = 37 donc
a = 37/3
Ex : Calculer les nombres réels a et b sachant que les valeurs numériques du
polynôme
ax2 – bx – 2
pour x = 1 et pour x = -1 sont respectivement -3 et 2
réponse :
a =2 et b = 3
Loi du reste de la division par ( x – x0 )
Le reste de la division d’un polynôme entier en x par ( x – x0 )
est égal à la valeur numérique du polynôme pour x = a.
Démonstration :
P(x) = (x – x0 ) Q(x) + reste
Avec le degré du reste strictement inférieur à celui de ( x – x0 ) càd
De degré zéro (autrement dit une constante)
Soit x = x0
En remplaçant dans l’égalité précédente , on obtient : P( x0 ) = 0 + reste
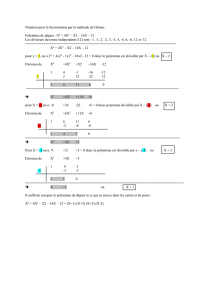
Ex : Le reste de la division de
P(x) = x 3 + 5x2 + 11x – 6 par ( x - 2 ) est P(2) = 8 – 20 + 22 – 6 = 4
Le reste de la division de
Q(x) = x2 - 2x + 5 par ( x + 3 ) est Q(-3) = 9 + 6 + 5 = 20
Conséquence :
Une CNS pour qu’un polynôme entier en x soit divisible par ( x – x0 ) est que sa
valeur numérique soit nulle pour x = x0
Démonstration : CNS est le reste nul.
Ex : P(x) = x2 - x – 6 n’est pas divisible par ( x – 2 )
P(x) = x 3 + 2a x2 + 2a2 x + a3 est divisible par ( x + a )
Remarque
Calculons (x + 2) . (x - 3)
Cela donne : x(x – 3) + 2(x – 3) = x2 - 3x + 2x – 6 = x2 - x - 6
Les racines de x2 - x – 6 sont -2 et +3
En effet les valeurs numériques P(-2) et P(+3) sont nulles !!!!