Chapitre 7 TS 2 Fonctions logarithmes et fonctions associées I – La

Chapitre 7 TS 2
1
Fonctions logarithmes et fonctions associées
I – La fonction logarithme népérien
Introduction :
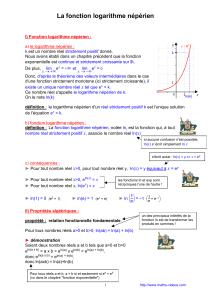
Nous savons que la fonction exp :
 Est définie, continue, et strictement croissante sur
 Vérifie
0lim 
x
xe
et
x
xelim
,
Donc pour tout réel b strictement positif, l’équation
bex
a une unique solution a dans .
Définition :
 Pour tout réel b strictement positif, on appelle logarithme népérien de b l’unique
solution de l’équation (d’inconnue a)
bea
. On le note
bln
.
 La fonction logarithme népérien est la fonction définie sur
;0
par
xx ln
.
Remarque fondamentale :
(
0b
et
ba ln
) équivaut à
bea
.
 Pour tout réel x :
xexln
car
abea lnln
.
 Pour tout
0x
:
xe x
ln
car
bee ab 
ln
.
On dit que exp et ln sont des fonctions réciproques.
01ln 
car
1
0e
.
1ln e
car
ee 
1
.
II – Propriétés algébriques
Propriété fondamentale : Preuve 1
Pour tous réels
0a
et
0b
baba lnln)ln( 
.
Propriétés : Preuve 2
Pour tous réels
0a
et
0b
:
b
bln
1
ln 
.
ba
b
alnlnln 
.
ananln.ln 
, n entier relatif.
III – Etude de la fonction ln
Théorème : Preuve 3
La fonction ln est continue et dérivable sur
;0
. Pour tout réel
0x
:
x
x1 'ln 
.
Propriétés : Preuve 4
 ln est strictement croissante sur
;0
.
 Pour tous réels a et b strictement positifs :
ba 
ssi
ba lnln 
.

Chapitre 7 TS 2
2
ba 
ssi
ba lnln 
.
Propriété :
Soit u une fonction strictement positive définie sur un intervalle I.
 u et ln u ont les mêmes variations.
 si de plus u est dérivable sur J alors ln u est dérivable sur I et, pour tout x de I,
)( )('
')(ln xu xu xu 
ou encore
u
u
u' 'ln 
.
Propriété fondamentale : Preuve 5
Soit une fonction f définie et dérivable sur
;0
telle que :
 pour tous a et b dans
;0
)()()( bfafabf
,
1)1(' f
,
Alors
lnf
.
Théorème : Preuve 6
x xlnlim
;
x xlnlim 0
.
Propriétés : Preuve 7
1
1ln
lim0
xx x
.
 Pour x proche de 0 :
xx  )1ln(
.
Tableau de variation :

Chapitre 7 TS 2
3
Courbe :
L’axe des ordonnées est asymptote à la courbe de ln.
Théorème : Preuve 8
0
ln
lim 
xx x
et
0lnlim
0 xx x
; on admet que ce théorème se généralise et on retient la règle
« à l’infini, les puissances de x l’emportent sur le logarithme de x ».
Exemples :
0
5100²4 ln
lim 
xx x
et
0ln²..2,0lim
0 xx x
car les puissances de x l’emportent sur le
logarithme de x.
IV – Puissance d’un réel strictement positif
1) Introduction
Nous savons que, pour tout réel a strictement positif et tout entier naturel n :
ananlnln 
.
Alors
ann ea ln
. Depuis peu, on sait que
exx ee ln
.
Définition :
Pour tout réel a strictement positif et pour tout réel b :
abb ea ln
.

Chapitre 7 TS 2
4
Remarque :
Cette définition étend au réels celle donnée avec des exposants naturels. Les propriétés de
calcul sur les puissances à exposants entiers seront encore valables.
Exemples :
4,2955ln1,21,2  e
.
03,07 7ln8,18,1   e
.
2) Fonction racine nième
La fonction
n
xxf :
définie sur
;0
, avec n un entier naturel non nul. Elle est continue
sur
;0
et strictement croissante sur
;0
;
0)0( f
et
)(lim xf x
.
D’après le corollaire du théorème des valeurs intermédiaires, pour tout réel positif a,
l’équation
axn
admet une unique solution b dans
;0
.
Définition :
Pour tout réel positif a et pour tout naturel n non nul, l’unique nombre positif b solution de
l’équation
axn
est appelé racine nième de a. On note
nab 
.
Remarque :
0a
et
0b
abn
ssi
nn
nab 11
)( 
ssi
nn
nab 11
ssi
n
ab 1
donc
n
naa 1
.
Exemples :
3999 2
1
2
.

Chapitre 7 TS 2
5
210241024 10
1
10 
car
1024210 
.
Définition :
La fonction f définie sur
;0
par
nxxf )(
où n est un entier naturel non nul est appelée
fonction racine nième.
Propriétés : Preuve 9
 f est continue sur
;0
.
 f est strictement croissante sur
;0
.
n
xxlim
.
 f est dérivable sur
;0
et, pour tout
0x
,
1
1
1
)('  n x
x
xf
.