les ts au pays imaginaire les ts au pays imaginaire

1111
Chapitre
LES TS AU PAYS IMAGINAIRELES TS AU PAYS IMAGINAIRE
1 INTRODUCTION
1.1 Un nouveau décor
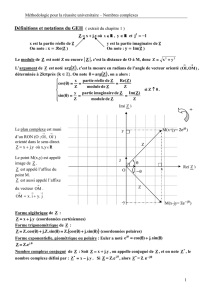
C R
x+iy x
y
z=x+iy M
(x;y)z
M+i
M(x;y)
z=x+iy
LYCÉE BLAISE PASCAL
1
S.DELOBEL
M.LUITAUD

2Chapitre 11. Les TS au pays imaginaire
(O;~u , ~v)
z=x+iy M(x;y)M(x;y)
z=x+iy zMm M
(O;~u) (O;~v)
A(2 ; 3) A
2+3i
z=x+iy
x y
2+3i2+3i
z=x+iy ~wx
yz~w
~wx
yz=x+iy
A2−3i B(−1+2i)C zC= 2i
−→
w(1 + 3i)−→ t2−i
−→
s−→ w−→ t−→ s
1.2 Premières propriétés
−−→
AB zB−zA
−→
w1z−→
w1−→
w2z−→
w2λ
−→
w1+−→ w2z−→
w1+z−→ w2
λ−→ w1λz−→
w1

Cours de Terminale S 3
I zI=zA+zB
2
zG=zA+zB+zC
3
( ; ~u , ~v )
zA= 3 + i zB=−1−i zC= 2i zD= 4 + 4i
2 DISTANCES ET ANGLES
2.1 Repérage polaire, module et arguments
M
(x;y) [r;θ]
r OM θ −→ u;−−→ OM
2π
x=rcos θ y =rsin θ
r r =OM =px2+y2
z=x+iy
z=rcos θ+ir sin θ
z=r(cos θ+isin θ)~u
~v
M
x
y
r
θ
z z =r(cos θ+isin θ)
z
r z θ
z=x+iy |z|=px2+y2
z z 6= 0 arg(z)
(−→ u;−−→ OM)M z

4Chapitre 11. Les TS au pays imaginaire
z1= 2 cos 4π
3+isin 4π 3
z2=√3cos −π
6+isin −π 6
z3= 1 + i√3
z4= 2 −2i
2.2 Propriétés du module et de l’argument
zz = Re(z)2+ Im(z)2
z∈Czz =|z|2
z
|z|=|z|arg(z) = −arg(z) [2π]
|−z|=|z|arg(−z) = arg(z)+π[2π]
M(z)
r
θ
M0(z)
r
−θ
M00 (−z)
r
θ+π
z
zarg(z) = 0 [2π] arg(z) = π[2π]z= 0
zarg z=π
2[2π] arg z=−π 2[2π]z= 0

Cours de Terminale S 5
z z0
|z×z0|=|z|×|z0|arg(z×z0) = arg(z) + arg(z0) [2π]
n|zn|=|z|narg(zn) = narg(z) [2π]
z=r(cos θ+isin θ)z0=r0(cos θ0+isin θ0)
z×z0
zz0
z z0
z
z0
=|z|
|z0|
arg z
z0= arg(z)−arg(z0) [2π]
z=z
z0×z0
z=z3×z4z3z4
z
(1 + i)8
zn= (1 + i)nn zn
|z+z0| 6=|z|+|z0|arg(z+z0)6= arg(z) + arg(z0)
cos (a±b) = cos acos b∓sin asin bsin (a±b) = sin acos b±sin bcos a