étude de la continuité et de la dérivabilité des fonctions circulaires

Chapitre 1
ÉTUDE DE LA CONTINUITÉ ET DE LA DÉRIVABILITÉ
DES FONCTIONS CIRCULAIRES
Annexe
Mise en place des fonctions circulaires
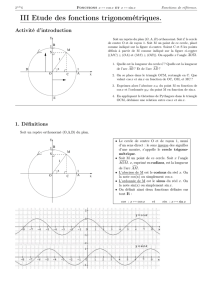
. Dans le plan euclidien orienté muni d'un repère orthonormé direct
(O,~i, ~j), on considère le cercle C de centre O et de rayon 1.
. Etant donné x ∈ R, on place, sur le cercle C , le point M tel que
−−→
\
x est une mesure de l'angle orienté (~i, OM ).
. L'abscisse de ce point est appelée cosinus de x, et est notée
cos(x), son ordonnée est appelée sinus de x, et est notée sin(x).
On appelle fonction cosinus (resp. fonction sinus), et on note cos (resp. sin), l'application qui,
à tout réel x, associe son cosinus (resp. son sinus).
Par construction, ces fonctions sont 2π -périodiques, le sinus étant de plus impair et le cosinus pair.
C'est encore cette construction (ainsi que le théorème de Pythagore) qui justie l'identité :
∀ θ ∈ R,
cos2 (θ) + sin2 (θ) = 1
1
Deux formules aussi connues qu'utiles
Parmi les nombreuses autres formules de trigonométrie, citons les fameuses :
∀ (a, b) ∈ R2 , cos(a + b) = cos(a) cos(b) − sin(a) sin(b),
∀ (a, b) ∈ R2 , sin(a + b) = sin(a) cos(b) + cos(a) sin(b).
Comme celles-ci vont être utiles pour établir certaines propriétés du sinus et du cosinus, commençons par les montrer.
Pour cela, xons deux réels a et b, et plaçons-nous de
nouveau dans le plan euclidien, muni d'un repère orthonormé direct (O,~i, ~j). Considérons alors le cercle C de
centre O et de rayon 1, et, sur ce cercle, les points A et
B choisis de sorte que a soit une mesure de l'angle orienté
−→
−→
−−→
\
[
(~i, OA) et b une mesure de (OA, OB).
−−→
\
On remarque alors que a+b est une mesure de (~i, OB).
Par conséquent, dans le repère (O,~i, ~j), B a pour coordonnées (cos(a + b), sin(a + b)).
Cependant, si l'on note ~k le vecteur obtenu en faisant
−→
−→
subir à OA la rotation d'angle + π2 , on voit que (O, OA, ~k)
est un autre repère orthonormé direct du plan, et, dans ce
repère, B a pour coordonnées (cos(b), sin(b)).
En outre, dire que les coordonnées de A dans (O,~i, ~j) sont (cos(a), sin(a)) revient à écrire l'égalité vectorielle :
−→
OA = cos(a)~i + sin(a)~j,
π ~
π ~
i + sin a +
j.
laquelle impose que ~k = cos a +
2
2
De plus, la construction des fonctions sinus et cosinus garantit également que :
π
π
π
π
= − cos a +
− π = − cos a −
= − cos
− a = − sin(a),
cos a +
2
2
2
2
π
et, de même, que sin a +
= cos(a).
2
~
~
Par conséquent, k = − sin(a)i + cos(a)~j .
−−→
Du coup, on dispose de deux écritures du vecteur OB :

 cos(a + b)~i + sin(a + b)~j
−−→ 
OB =
→

 cos(b)−
OA + sin(b)~k = cos(b) cos(a)~i + sin(a)~j + sin(b) − sin(a)~i + cos(a)~j .
L'unicité des coordonnées d'un vecteur dans une base donnée impose alors les deux égalités suivantes :

 cos(a + b) = cos(a) cos(b) − sin(a) sin(b)

sin(a + b) = sin(a) cos(b) + cos(a) sin(b)
2
Continuité
Pour justier la continuité des fonctions sinus et cosinus sur R, nous allons préocéder en plusieurs étapes :
1. Une inégalité fondamentale
Dans un premier temps, nous allons montrer que, pour tout x ∈ R, | sin(x)| 6 |x|, ce qui, selon les valeurs prises
par x, est plus ou moins
:
i πdicile
πh
• Pour tout x ∈ R \ − , , on remarque simplement que :
2 2
|x| >
π
> 1 > | sin(x)|.
2
• Signalons également que cette
est vériée, sous forme d'égalité, lorsque x = 0.
i inégalité
πh
• Considérons, à présent, x ∈ 0, .
2
Pour des raisons presque évidentes de convexité du
disque contenu dans le cercle unité, il apparaît clairement que le triangle OM I a une aire inférieure à celle
de la portion du disque unité située entre les demidroites [OI) et [OM ).
OI × sin(x)
sin(x)
=
,
Or l'aire du triangle OM I vaut
2
2
tandis que la surface de la portion de disque considérée est proportionnelle à l'écart angulaire x : pour un
écart angulaire de 2π , cette aire serait de π (aire du
x
x×π
= .
disque entier), donc, pour x, elle vaut :
2π
2
Par conséquent, 0 6 sin(x) 6 x.
i π h
• Enn, dans le cas où x ∈ − , 0 , on peut se contenter de remarquer que, puisque la fonction sinus est
2
impaire :
| sin(x)| = − sin(x) = sin(−x) 6 −x = |x|.
|
{z
}
car 0<−x< π2
Ainsi, l'inégalité | sin(x)| 6 |x| est vériée pour tout x ∈ R.
2.
Continuité du sinus en 0
En réécrivant ce qui précède sous la forme :
∀ x ∈ R,
0 6 | sin(x)| 6 |x|,
on remarque aisément que, d'après le théorème des gendarmes, cet encadrement impose que sin(x) −→ 0.
x→0
En d'autres termes, la fonction sinus est continue en 0.
3.
Continuité du cosinus en 0
Comme, pour tout x ∈ R, cos2 (x) + sin2 (x) = 1, et puisque
la restriction du cosinus à − π2 , π2 prend ses valeurs
q
dans R+ , il vient, pour tout x ∈ − π2 , π2 : cos(x) = 1 − sin2 (x).
Des opérations classiques (opérations algébriques et composition) sur les limites permettent d'en déduire que
cos(x) −→ 1, autrement dit que la fonction cosinus est continue en 0.
x→0
4.
Continuités globales
Soit x0 ∈ R.
Pour tout h ∈ R, sin(x0 + h) = sin(x0 ) cos(h) + cos(x0 ) sin(h). Par conséquent, d'après les limites déterminées
précédemment :
sin(x0 + h) −→ sin(x0 ) × 1 + cos(x0 ) × 0 = sin(x0 ).
h→0
Autrement dit, la fonction sinus est continue en x0 .
Ceci étant valable pour tout réel x0 , on vient d'établir la continuité de la fonction sinus.
On procède de la même manière pour justier la continuité de la fonction cosinus sur R.
3
Dérivabilité
La démarche globale est proche de celle suivie pour la continuité... avec un point de départ "amélioré" :
1. Une nouvelle inégalité fondamentale
i π
2
sin(x)
πh
, cos(x) 6
6 1.
2
i π hx
• Considérons, tout d'abord, un réel x de l'intervalle 0, .
2
h
i
Montrons que, pour tout x ∈ − , 0 ∪ 0,
Reprenons une approche géométrique analogue à celle
utilisée précédemment : en plus d'être supérieure à
celle du triangle OM I , l'aire de la portion de disque
comprise entre les demi-droites [OI) et [OM ) est inférieure à celle du triangle OT I . Or cette dernière vaut
IT
OI × IT
=
, et la distance IT vérie, d'après le
2
2
théorème de Thalès :
sin(x)
cos(x)
=
IT
OI
Par conséquent, IT =
OM
=
.
OT
sin(x)
.
cos(x)
De notre comparaison de surfaces, on déduit donc l'encadrement :
sin(x)
x
1
sin(x)
sin(x)
6 6 ×
, ou encore sin(x) 6 x 6
.
2
2
2 cos(x)
cos(x)
En particulier, on a : sin(x) 6 x et x 6
x cos(x) 6 sin(x).
Enn, puisque x > 0, on conclut :
sin(x)
, et comme cos(x) > 0, on déduit de cette dernière inégalité que
cos(x)
cos(x) 6
sin(x)
6 1.
x
• On peut, comme précédemment, utiliser la
parité
des fonctions x 7→ cos(x) et x 7→
encadrement reste valable pour tout x ∈ − π2 , 0 .
2.
sin(x)
x
pour justier que cet
Dérivabilité du sinus en 0
De l'encadrement précédent on déduit, par le théorème des gendarmes :
sin(x)
−→ 1
x x→0
Or, comme sin(0) = 0, le quotient ci-dessus n'est autre que le taux de variation de la fonction sinus en 0.
Ainsi, on vient d'établir que la fonction sinus est dérivable en 0, et que sin0 (0) = 1.
3.
Dérivabilité du cosinus en 0
Ici, on s'intéresse au comportement, au voisinage de 0, de x 7→
Or, pour tout x ∈ R :
cos(x) − cos(0)
=
=
=
=
=
=
cos(x) − cos(0)
.
x−0
cos(x) − 1
x
cos 2 ×
−1
2
x
x cos2
− sin2
− 1 d'après la formule cos(a + b) = · · · 2 2
x
x 1 − sin2
− sin2
−1
2
2x 1 − 2 sin2
−1
x 2
−2 sin2
2
4
Ainsi, pour tout x ∈ R∗ :
sin2
cos(x) − cos(0)
= −2 ×
x−0
x
x
2
= −2 ×
sin2
x
2
x 2
2
×
x 2
2
x
x
=− ×
2
x
2
sin
x
2
!2
.
Par composition(s) de limites, la dérivabilité de la fonction sinus en 0 garantit que :
x
2
sin
x
2
et donc, par produit de limites :
!2
−→ 1,
x→0
cos(x) − cos(0)
−→ 0.
x→0
x−0
Cela montre que la fonction cosinus est dérivable en 0 et que cos0 (0) = 0.
Remarque : La forme indéterminée levée dans ce calcul est même plus précise que celle qu'indique le taux de
variation de la fonction cosinus en 0. En eet, on a établi que :
cos(x) − 1
1
−→ −
x→0
x2
2
4.
Dérivabilités globales
Soit x0 ∈ R.
Pour tout h ∈ R∗ , on a :
sin(x0 + h) − sin(x0 )
(sin(x0 ) cos(h) + cos(x0 ) sin(h)) − sin(x0 )
cos(h) − 1
sin(h)
=
= sin(x0 ) ×
+ cos(x0 ) ×
.
h
h
h
h
Les limites déterminées dans les études précédentes permettent d'en déduire que :
sin(x0 + h) − sin(x0 )
−→ sin(x0 ) × 0 + cos(x0 ) × 1.
h→0
h
En d'autres termes, la fonction sinus est dérivable en x0 , et sin0 (x0 ) = cos(x0 ).
Ceci étant valable pour tout x0 ∈ R, la fonction sinus est dérivable sur R, et sin0 = cos.
On montre, de façon analogue, que cos est dérivable, et cos0 = − sin.
5