Les nombres complexes

C
i i2=−1
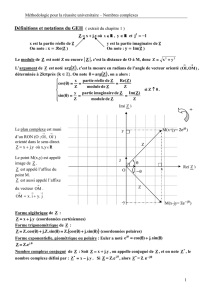
z z =x+iy x
y
x z Re(z)
y z Im(z)
C
z=x+iy
z=x+iy
z0=x0+iy0
z+z0=x+x0+i(y+y0)
z=x+iy
z0=x0+iy0
zz0=xx0−yy0+i(xy0+yx0)
C
R
z−z
z+ (−z)=0
z=x+iy −z=−x−iy
z z0
z−z0z−z0=z+ (−z0)
z=x+iy z0=x0+iy0
z−z0=x−x0+i(y−y0)
z
1
zz×1 z= 1
z=x+iy 1
z=x−iy x2+y2
z z0z0
z z0z
z0
z
z0=z×1 z0
C R
P(O, −→ e1,−→ e2)
z=x+iy
z(x;y)z(z)
z ~v(x;y)z ~v
~v(z)
P
(O;−→ e1)
(O;−→ e2)

~u(z)~v(z0)~u +~v(z+z0)
(z) (z0)−→(z0−z) [ ] z+z0
2
(A1, α1),(A2, α2), ..., (An, αn)n
zA1, zA2, ... , zAn
n
P
k=1
αk6= 0
zG=
n
P
k=1
αkzAk
n
P
k=1
αk
z=x+iy
¯z=x−iy
(z) ( ¯ z0)
(z)7→ (¯ z0)
(O,~ i)
z z0
z=z
z+z0=z+z0
z×z0=z×z0
z6= 0 1
z=1 z
z06= 0 z
z0=z
z0
zn= (¯z)nn∈Z
z
Re(z) = z+z
2Im(z) = z−¯z 2i
z
z∈Rz=z
z∈iRz=−z
z=x+iy |z|=√z¯z
|z|=px2+y2
|zz0|=|z||z0|
|z
z0|=|z| |z0|
Re(z)6|z|
|z+z0|6|z|+|z0|
z=x+iy arg(z)
−→
e1,−−→ OMz
]−π;π]
z=x+iy
θ2π z
cos θ=x
px2+y2sin θ=y px2+y2
z=|z|(cos θ+isin θ)
z ρ
θ z z =ρ(cos θ+isin θ)
z=r(cosθ +isin θ)r > 0|z|=r
arg(z) = θ[2π]
z z0
arg(¯z) = −arg(z)[2π]
arg(−z) = arg(z) + π[2π]
arg(zz0) = arg(z) + arg(z0)[2π]
arg 1
z=−arg(z)[2π]
arg z
z0= arg(z)−arg(z0)[2π]
arg (zn) = narg(z)[2π]n∈Z
A(zA)B(zB)−→ e1,−−→ AB=
arg (zB−zA) [2π]
A(zA)B(zB)C(zC)D(zD)
−−→
AB, −−→ CD= arg zD−zC
zB−zA[2π]

n θ
(cos θ+isin θ)n= cos nθ +isin nθ
z ρ
θ z z =ρeiθ
z=ρeiθ z0=ρ0eiθ0
¯z=ρe−iθ
zz0=ρρ0ei(θ+θ0)
z
z0=ρ ρ0ei(θ−θ0)
zn=ρneinθ n∈Z
θ
cos θ=eiθ +e−iθ
2sin θ=eiθ −e−iθ 2i
C
a b c a
az2+bz +c= 0 z
C
C
∆ = b2−4ac az2+bz +c= 0
az2+bz +c=a z+b
2a2
−∆
4a2!
∆>0az2+bz+c= 0 z1=−b−√∆
2a
z2=−b+√∆
2a
∆=0 az2+bz+c= 0 z0=−b
2a
∆>0az2+bz +c= 0
z1=−b−i√−∆
2az2=−b+i√−∆ 2a
z2=z1
Caz2+bz +c
M(z)|z−a|=r a ∈Cr>0
A(a)r
M(z)|z−a|=|z−b|a∈C
b∈C
M(z) arg(z−a) = θ a ∈C
θ∈R−→ v
(−→ e1,−→ v) = θ[2π]
M(z) arg z−b
z−a=π 2a∈C
b∈Cz6=a z 6=b
z7→ z0
z0=z+b b ∈C
z
z0z0=z+b−→ u b
z0−ω=k(z−ω)k∈R∗ω∈C
z
z0z0−ω=k(z−ω)k∈R∗ω∈C
kΩω
z0−ω=eiα(z−ω)α∈Rω∈C
z
z0z0−ω=eiθ (z−ω)θ∈Rω∈C
Ωω θ