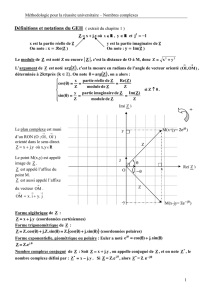
1 Nombres réels

o
•N={0,1,2, . . .}
•Z={. . . , −2,−1,0,1,2, . . .}
•Q={p
q, p ∈N, q ∈N∗}
•R
•C
0N∗=
{1,2,3, . . .}
+
R+= [0,+∞[R∗
+=]0,+∞[
R R
Q
R
+∞ −∞
[a, b] = {x∈R|a≤x≤b},[a, b[= {x∈R|a≤x<b},[a, +∞[= {x∈R|a≤x},
]a, b] = {x∈R|a<x≤b},]a, b[= {x∈R|a<x<b},]a, +∞[= {x∈R|a<x},
]− ∞, b] = {x∈R|x≤b},]− ∞, b[= {x∈R|x<b},]− ∞,+∞[= R.

]−2,5] = {x∈R:−2< x ≤5}
[0,10] = {x∈R: 0 ≤x≤10}
[π, +∞[= {x∈R:x≥π}
a∈R{a}
{a}= [a, a]
x
|x|=(x, x ≥0,
−x, x < 0.
x y
d(x, y) = |x−y|.
|x|x0
|x| ≥ 0
|xy|=|x|.|y|
|x|= 0 ⇔x= 0
|x| ≤ a⇔ −a≤x≤a
|x|= max(−x, x)
Rx, y ∈R
|x+y|≤|x|+|y|,
x y

x y
x+y
|x|−|y|≤ |x−y|.
x∈R
xbxc
bxc
bxc ≤ x < bxc+ 1,
x−1<bxc ≤ x.
x, y ∈Rm, n ∈Z
n > 0xnx n
n < 0xn=1
x−n
n= 0 x6= 0 x0= 1 00
x≥0x
x√x
x < 0x
(xy)n=xnyn, xn+m=xnxm,(xn)m=xnm,
(√x)2=x, √x2=|x|,√xy =√x√y.
a, b ∈R
(a+b)2=a2+b2+ 2ab,
(a−b)2=a2+b2−2ab,
(a+b)(a−b) = a2−b2.

x∈R(E)
(E)x2+ 2 = 0
(E) 3x+ 2 = 10
(E) (x−1)(x+ 4)(x+ 3) = 0
(E) cos x= 1/2
(E)
a=b⇔a2=b2
x3ln(x)=3x2ln(x)
{0,1,3}
ax2+bx +c= 0, x ∈R
∆ := b2−4ac
∆>0−b−√∆
2a−b+√∆ 2a
∆=0 −b
2a
∆<0
x y
a > 0
x≤y⇔ax ≤ay, x < y ⇔ax < ay,
a < 0
x≤y⇔ax ≥ay, x < y ⇔ax > ay.
x y
x≤y⇔1
x≥1 y, x < y ⇔1 x>1 y.

x≤y⇔ex≤ey, x ≤y⇔√x≤√y, x ≤y⇔ln x≤ln y
pln(1 + x2)>1x∈R
xln x−2 ln2x−4 ln(x) + xln2x > 2 ln2x
P(x) = ax2+bx+c
P(x)a
∀x∈I, f(x)≤g(x),
f g I
u=g−f
u
∀x∈R, ex≥1 + x
AR
M A ∀x∈A, x ≤M
m A ∀x∈A, x ≥m
R