Nombres complexes Fiche 1 Cours et exercises d'application

Fiche 1 : Nombres complexes BAC : Sc & Maths Mr : OUNI Anouar [e-mail]
1
Prof: Mr OUNI Anouar
BAC :Maths & Sciences
A-S: 2013-2014
Nombres complexes
Cours et exercises d'application
Fiche 1
-I- Ensemble des nombres complexes:
Théorème (admis) et définitions :
Il existe un ensemble noté appelé ensemble des nombres complexes, qui vérifie les propriétés suivantes:
 L'ensemble contient l'ensemble des nombres réels :
 L'addition et la multiplication dans ont les mêmes propriétés que celles dans
 Il existe dans un nombre complexe notée
i
tel que
21i
 Pour tout nombre complexe z il existe un unique couple (a,b) de réels tel que : z=a+i b
Forme algébrique d'un nombre complexe :
L'égalité z=a+i b est la forme algébrique du nombre complexe z (dite aussi forme cartésienne) .
Le réel a s'appelle la partie réelle de z qu'on note Re(z) et le réel b s'appelle la partie imaginaire de z qu'on
note Im(z)
Exemple : Re(3-5i)=3 et Im(3-5i)=-5 ; Re(2i)=0 et Im(2i)=2 ; Re(-
2
)=-
2
et Im(-
2
)=0 …etc
 Un nombre est dit réel si et seulement si sa partie imaginaire est nulle:
Im( ) 0zz  
 Un nombre complexe est dit imaginaire pur réel si et seulement si sa partie réelle est nulle :
Re( ) 0z z i   
 Le 0 est le seul nombre complexe qui est réel et imaginaire pur
Calculs avec les complexes :
-1) On a par convention :
21i
Astuce N°1 :
k
0 4 8 12 4
1 5 9 13 4 1
2 6 10 14 4 2
3 7 11 15 4 3
... 1
...
... 1
...
k
k
k
k
i i i i i
i i i i i i
i i i i i
i i i i i i
Application :
 Le reste de la division euclidienne de 2013 par 4 est 1 d’où :
2013 1 i i i
car
2013 4 503 1  
 Le reste de la division euclidienne de 171 par 4 est 3 d’où :
171 3 i i i  
car
171 4 42 3  
-2) Les calculs se font comme avec les nombres réels :
-a) Exemple : " Somme et produit de deux nombres complexes "
2
1
(5 2 ) ( 3 4 ) 5 2 3 4 5 3 2 4 2 2
( ) ( 3 4 ) 3 4 3 4
15 20 6 8
15 20 6
5 5 2 5 2 2
i i i i i i
i i i
i i i
ii
i i i
8 7 26i   
-b) Egalité de deux nombres complexes :
a a'
' '
b b'
a ib a ib 
Exemple :
3
3 4
4
x
x iy i y
particulier a+ib=0 a=b=0En 

Fiche 1 : Nombres complexes BAC : Sc & Maths Mr : OUNI Anouar [e-mail]
2
Le plan complexe :
On considère un plan rapporté à un repère orthonormal
,,o u v
.Ce plan est le plan complexe dès lors que :
 A tout point M de coordonnées
,
MM
xy
on associe le complexe
MM
x iy
,noté
M
z
et l'affixe de M.
 A tout complexe x+iy ( avec x et y des réels) on associe le point M dont le couple de coordonnées
est (x,y) , noté M(x+iy) et appelé image du nombre complexe x+iy
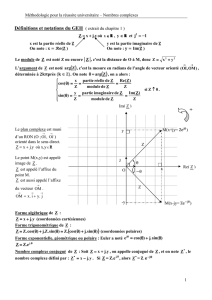
Exemple :Dans le plan complexe rapporté à un repère orthonormal
,,O OI OJ
.Représenter les points M
et N d'affixes respectives 3+2i et 3-i ; et placer le point K image de nombre complexe -2+2i.
Conséquence : affixe d'un vecteur .
Pour tout vecteur
w
il existe un point M et un seul tel que :
OM w
.C'est pourquoi l'affixe z du point M est
aussi l'affixe du vecteur
w
.
Pour tous points A et B , il existe un seul point M tel que :
OM AB
.Le point M et le vecteur
AB
ont donc
pour coordonnées
,
B A B A
x x y y
et pour affixe
B A B A
x x i y y  
.De
B A B A B B A A B A
x x i y y x iy x iy z z        
il résulte que
AB
a pour affixe
BA
zz
.
On écrit :
()BA aff AB z z
Exemple :
Soit A(-1,3) et B(4,7) .Alors :
1 3 et z 4 7
AB
z i i    
4 7 1 3 5 4
BA
AB
z z z i i i        
Vocabulaire :
 L'axe des abscisses est aussi dénommé "axe réel" car il est l'ensemble des points pour lesquels y=0
 L'axe des ordonnées est aussi dénommé "axe imaginaire" car il est l'ensemble des points pour
lesquels x=0
-II- Nombre complexe conjugué:
Soit
z x iy
un nombre complexe avec x et y réels. Le conjugué de z est le nombre complexe
z x iy
Exemple :
3 2 3 2 ; 4 4 ; 2 2 ; 3 3i i i i i i        
Astuce N°2: Soit z un nombre complexe :
 z est réel si et seulement si
zz
:
z z z  
 z est imaginaire pur si et seulement si
zz
:
z z z i    
A SAVOIR :
Opérations sur les nombres complexes conjugués : Pour tous complexes z et z' on a :
*
*
' ' 11
z
. .
z z' ' z'
''
n
n
n
z z z z
zz zz
zz zz
zz
zz

Fiche 1 : Nombres complexes BAC : Sc & Maths Mr : OUNI Anouar [e-mail]
3
Produit
.zz
: Soit z=x+iy , avec x et y réels , on a :
22 réel positif z.z= nombrexy 
Astuce N°3: " Inverse d'un nombre complexe non nul "
Soit z=x+iy un nombre complexe non nul .
Pour déterminer la forme algébrique de nombre complexe de
11
Zz x iy
, on multiplie le numérateur et
le dénominateur de
1
Zz
par
z
:
22
2 2 2 2 2 2
22
Re( )
1
.Im( )
x
Zxy
z x iy x y
Zi
y
z x y x y x y
zz Zxy
Exemple : Mettre sous forme algébrique les nombre complexe
43
35
i
Zi
et
1
'Zi
2
2
2
43
4 3 12 20 9 15 3 29 3 29
3 5 3 5 34 3
35
35 4 34
35
i
i i i i
i
Zi
i
ii
i
2
1
'.11iiii
i
Zi
i i i
Astuce N°4: mettre sous forme algébrique :
2 2 13 7 1
1 ; 1 ; 1 ; 1 et 1i i i i i i
22
1 =1i
2
2. 1 . ii
22
2
1=1
i
i
2
2. 1 . ii
6
13 12 2 6 66
64 1
3
7 6 2 3 3 32
8
2
2
2
2
1 = 1 . 1 1 . 1 2 . 1 2 . . 1 64 64
1 = 1 . 1 1 . 1 2 2 . . 1 8 . 1 8 8 8 8
11
12
11 11
1
1
2
i
i i i i i i i i i i
i i i i i i i i i i i i i
ii
i
ii
i
i
i  2ii
-III- Application: Recherche d'ensemble des points "Méthode analytique"
A SAVOIR :
-1) les droites dans le plan :
Dans le plan complexe rapporté à un repère orthonormal
,,O OI OJ
, l'ensemble des points
,M x y
formant la droite D peut se représenter par une équation de la forme :ax+by+c=0 où a , b et c sont des
constantes telles que (a,b)≠(0,0). Dans ce cas,
2
, / 0D x y ax by c    
Cas particuliers :
 Dans le plan, une droite D parallèle à l'axe des abscisses (horizontale) a une équation de la forme:
00
avec yyy
 De même, une droite D parallèle à l'axe des ordonnées (verticale) a une équation de la forme :
00
avec xxx
Toute droite admet une équation du type y=ax+b avec a le coefficient directeur (ou pente) de la droite et b
l'ordonnée à l'origine.
Remarque : l'ordonnée à l'origine est le point d'intersection de la droite avec l'axe des ordonnées.

Fiche 1 : Nombres complexes BAC : Sc & Maths Mr : OUNI Anouar [e-mail]
4
Définition: soit
, et ,
A A B B
A x y B x y
alors le coefficient directeur de
la droite (AB) est défini par :
AB
AB
yy
axx
Propriétés :
 Si deux droites d: y=ax+b et d': y=a'x+b' sont parallèles,
alors a=a'
 Si deux droites d et d' sont perpendiculaires, alors
. ' 1aa 
(réciproque vraie)
Exercice :
Tracer la droite (AB) passant par A(1,2) et B(-2,3) et déterminer une équation cartésienne de (AB) .
L'équation cartésienne de la droite (AB) est de la forme :
y=ax+b avec a est la pente et b l'ordonnée a l'origine on a :
(1,2) ( ) . 2
( 2,3) ( ) . 3 2
1
2 3 2
1
2
13
2 3 1
encore : a= 1 2 3
17
2 2.33
33
23
3 1
AA
BB
AB
AB
A AB y a x b a b
B AB y a x b a b
a b a b a
yy
ou xx
bbdans
d’où une équation de (AB) est de la forme :
17
( ): 33 AB y x  
ou encore
3 7 0yx  
en écrit :
( ) ( , ) /3 7 0AB M x y Plan y x    
Remarque : la pente a est négatifs alors la droite est décroissante
-2) les cercles :
Equation cartésienne d'un cercle :
L'ensemble
22
2
00
( , ) / x x y y RE M x y Plan    
est le cercle de centre
00
,xy
et de rayon R
Exemple :
22
( , ) / 1 16E M x y Plan x y    
est le cercle de centre
1,0
et de rayon
16 4R
22
( , ) / 1M x y Plan x y
Est le cercle de centre
0,0O
et de rayon
1R
22
( , ) / 3M x y Plan x y       
22
( , ) / 5 3 0 5, 3 : pointM x y Plan x y un         

Fiche 1 : Nombres complexes BAC : Sc & Maths Mr : OUNI Anouar [e-mail]
5
Equation généralisé d'un cercle :
22
22
2 2 2 2
2 2 2 2
22
2 2 2
22
2
0 0 0
22
( , ) / 0
4
4
4
()
22
4
2 2 4 4 4
si = <0 E
pose
=
4
()
E M x y Plan x y x y
x y x y x x y y x y
xy
on
i
ii
22
2 2 2 2
4
si = =0 ,
4 2 2
44
( ) si = >0 est le cercle de centre , et de rayon R=
4 2 2 4
E
iii E
Exemple :
Déterminer les ensembles des points M suivants :
22
22
22
( , ) / 2 3 4 0
1
( , ) / 4 3 0
4
( , ) / 2 2 1 0
E M x y Plan x y x y
F M x y Plan x y x y
G M x y Plan x y x y
Solution :
22
22
22
22
22
2
( , ) / 2 3 4 0
2 3 4 4 3
44 1
( , ) / 4 3 0
4
1
4 3 4 24 3
46 est le cercle de centre 2, et de
0
rayon R= 6
4 4 2
( , ) / 2 2 1
0
0
2
E M x y Plan x y x y
E
F M x y Plan x y x y
F
G M x y Plan x y x y
2
2 4 1 2 2
,
4 2 2
0G