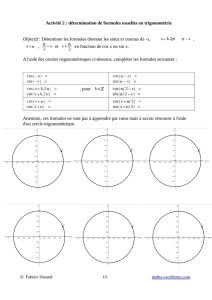
1 Complexes de modules 1 2 Formules de Moivre

NOMBRES COMPLEXES II Exponentielle imaginaire
1 Complexes de modules 1
•Notation. On note Ul’ensemble des complexes de module 1 : U=
•A retenir. Si z∈Ualors :
Pour θ∈R, on pose eiθ =
déf.
Définition
Exemple 1 — e2iπ
3=
•Valeurs à connaître. •ei0 = e2iπ = •eiπ
2
= •eiπ = •e−iπ
2
=
1. Si z∈Con a :
2. Si θ,θ0∈R,ona:
3. Pour tout θ∈R:
4. Pour tous θ,θ0∈R:
Théorème
Exercice 1 — Démontrer les points 3 et 4.
Exemple 2 — Trouver tous les z∈C∗tels que |z|=
1
z
=|z−1|.
2 Formules de Moivre et formules d’Euler
1. Formule de Moivre. Pour tout θ∈Ret tout n∈N:
2. Formules d’Euler. Pour tout θ∈R:
Théorème
Exercice 2 — Démontrer la formule de Moivre et les formules d’Euler.
• •
Théorème : Transformation de 1±eiθ
Exercice 3 — Démontrer ces deux formules en « factorisant par l’angle moitié ».
Exemple 3 — Soient p,q ∈R, calculer la partie réelle de eip +eiq. Que retrouve-t-on ?
3 Applications à la trigonométrie
Euler et linéarisation
•Objectif. Linéariser une expression de la forme cospxsinqx i.e. l’exprimer à l’aide de cosx,cos 2 x, cos 3 x..., et
sinx,sin2x, sin3x,... (sans puissances ni produits). Par exemple : cos2x=1 + cos2x
2
Deux ingrédients : 1. 2.
En pratique : pour linéariser cospxsinqx
Exemple 4 — Linéariser : a) sin5x.b) cos4xsinx
Moivre et « délinéarisation »
•Objectif. Effectuer la transformation inverse i.e. écrire cosnx (ou sinnx ) comme un polynôme en cosx et sinx
Deux ingrédients : 1. 2.
En pratique : pour « délinéariser » cosnx
Exemple 5 — Ecrire cos4xcomme un polynôme en cos xet sin x.
Calcul de sommes trigonométriques
Exemple 6 — Soit x∈R. Pour n∈N, calculer les sommes Cn=n
P
k=0
coskx et Sn=n
P
k=0
sinkx.