04. Quotients 5èA - copie

CH V QUOTIENTS
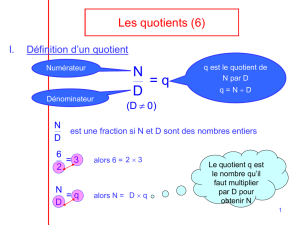
1. Quotient exact de deux entiers
A) Définition
• Le résultat d’une division s'appelle un quotient.
19 : 2 = 9,5
le dividende le diviseur le quotient exact de 19 par 2
multiplication à trou associée : 2 x ? = 19
• Le quotient exact est le nombre qui, multiplié par le diviseur redonne le dividende.
B) Ecriture fractionnaire d’un quotient
19 : 3 = 6,3333 . . . . 3 . . . .
ce n’est pas un nombre décimal.
19 : 3 ≈ 6 ,3 quotient approché au dixième près.
19 : 3 ≈ 6 ,33 quotient approché au centième près.
Le quotient exact de 19 par 3 se note par une fraction .
19 : 3 =
Je retiens :
x 3 = 2 / x 7 = 10 / x b = a
C) Fraction
Une fraction s’écrit avec 2 nombres entiers.
est une fraction ; n'est pas une fraction
D) Fraction et problème
Jean a 200 € d'économie. Il donne les 4/5 de son argent à son frère.
Combien lui donne-t-il ?
200 x = (200 : 5) x 4 200 x = (200 x 4) : 5 200 x = 200 x (4 : 5)
= 40 x 4 = 800 : 5 = 200 x 0,8
= 160 = 160 = 160
Jean donne 160 €.
19
3
2
3
10
7
a
b
13
27
13,5
27
4
5
4
5
4
5
le numérateur
le dénominateur
on calcule 1/5

2. Quotients égaux
A) 
Je retiens :
On ne change pas un quotient lorsqu’on multiplie son numérateur et
son dénominateur par un même nombre.
B)  ;  ; 
Je retiens : On peut toujours transformer une écriture fractionnaire en fraction.
C) 1835 : 1,2 =  ≈ 1 529
Pour diviser par un nombre décimal, on doit transformer la division pour que le diviseur
devienne entier.
3. Simplifier une fraction
A) Exemple
ou
on a simplifié par le nombre k
Je retiens Pour simplifier une fraction, on divise ses termes par un même nombre.
1
2
=2
4
=3
6
=4
8
=0,5
a
b
=a×k
b×k
1,2
15
=1,2 ×10
15 ×10
=12
150
0,2
0, 07
=0,2 ×100
0, 07 ×100
=20
7
8
2,5
=8×2
2,5 ×2
=16
5
1835
1,2
=1835 ×10
1,2 ×10
=18350
12
18
24
=18 : 6
24 : 6
=3
4
18
24
=6×3
6×4
=3
4
⧸
⧸
a×k
b×k
=a
b
⧸
⧸

B) Règles de divisibilité
Un nombre est divisible par 2 lorsqu'il se termine par 0 ou 2 ou 4 ou 6 ou 8.
Un nombre est divisible par 3 lorsque la somme de ses chiffres est dans la table des 3.
Un nombre est divisible par 4 lorsque le nbre formé par ses 2 derniers chiffres est dans la table des 4.
Un nombre est divisible par 5 lorsqu'il se termine par 0 ou 5.
Un nombre est divisible par 9 lorsque la somme de ses chiffres est dans la table des 9.
Un nombre est divisible par 10 ou 100 ou 1 000 . . . lorsqu'il se termine par 0 ou 00 ou 000 . . .
Un nombre est divisible par 25 lorsqu'il se termine par 00 ou 25 ou 50 ou 75.
C) Une fraction qu’on ne peut pas simplifier est irréductible.
est irréductible
4. Comparaison de quotients
A) Même dénominateur
≻
Lorsque des quotients ont le même dénominateur,
le plus petit est celui qui a le plus petit numérateur
B) Même numérateur
≺
Lorsque des quotients ont le même numérateur,
le plus petit est celui qui a le plus grand dénominateur.
C) Quotients quelconques : et
1°)
On réduit les quotients au
même dénominateur.
= /
donc :
≻
2°)
On calcule les quotients
= 0,8 et = 0,425
0,8 ≻ 0,425 donc
≻
3°)
On utilise un nombre
intermédiaire
≻ 0,5 et ≺ 0,5
donc
≻ !
3
4
13
20
7
20
13
20
13
12
4
5
17
40
4
5
4×8
5×8
=32
40
17
40
4
5
17
40
4
5
17
40
4
5
17
40
4
5
17
40
4
5
17
40

5. Proportion
Exemple 1
Deux cinquièmes des élèves du collège Camille Claudel sont externes.
La proportion des élèves externes est . Cela signifie que 2 élèves sur 5 sont externes.
On a aussi : = 40% 40% des élèves sont externes.
Exemple 2
On dort en moyenne 8 heures par jour.
Quelle est la proportion du temps passé à dormir ?
On dort 8 heures sur 24 h ➼ = =
La proportion du temps passé à dormir est 1/3.
2
5
2
5
=2×20
5×20
=40
100
8
24
8 : 8
24 : 8
1
3