Chap 15 Fonctions affines ( version prof)

Chap 15 Fonctions affines
I )Définition
Définition :Une fonction affine f est une correspondance qui associe à un nombre x l’unique nombre
!
ax +b
où a et b sont des nombres constants.
Elle se note :
!
f:xaax +b
Vocabulaire : Le nombre
!
ax +b
s’appelle l’image de x par la fonction f et il se note
!
f(x)
.
On écrit :
!
f(x)=ax +b
Ainsi pour déterminer l’image d’un nombre par la fonction f , on le multiplie par a puis on ajoute b au
résultat.
Remarques : :
• Lorsque b est égal à 0, la fonction f s’écrit :
!
f:xaax
.
Par conséquent, une fonction linéaire est une fonction affine particulière.
• Lorsque a est égal à 0, la fonction f s’écrit :
!
f:xab
.
On dit que f est une fonction constante.
Exemples :
1)
!
f:xa"3x"2
f est une fonction affine avec a égal à -3 et b égal à -2.
2)
!
h:xa3x2"5
h n’est pas une fonction affine ( à cause du terme
!
3x2
)
3)
!
i:xa2
3
x
i est une fonction affine avec a égal à
!
2
3
et b égal à 0. C’est aussi une fonction linéaire.
4)
!
g:xa"2,7
g est une fonction affine avec a égal à 0 et b égal à -2,7. g est une fonction constante.
II) Représentation graphique d’une fonction affine
Propriété (admise ) : Dans le plan muni d’un repère, la représentation graphique d’une fonction affine est
une droite non parallèle à l’axe des ordonnées.
Définitions : Soit (d) la droite représentative d’une fonction affine f telle que :
!
f:xaax +b
(avec a et b
nombres constants).
 Le nombre a s’appelle le coefficient directeur de la droite (d) ( de lui dépend l’inclinaison de la pente).
 Le nombre b s’appelle l’ordonnée à l’origine. ( C’est l’ordonnée du point d’intersection de la droite (d)
avec l’axe des ordonnées).
 La droite (d) a une équation de la forme :
!
y=ax +b
( Ce qui signifie qu’elle est constituée de tous les
points de coordonnées ( x ; y) avec y = f(x) ).

Exercice résolu : Dans un repère du plan, tracer la représentation graphique de la fonction f telle que :
!
f(x)="4x+3
.
• f est une fonction affine donc sa représentation graphique est une droite (d) non parallèle à l’axe des
ordonnées.
Cherchons les coordonnées de deux points de (d).
!
f(1) ="4#1+3="4+3="1
donc (d) passe par le point A( 1 ;-1)
!
f(0) ="4#0+3=0+3="3
donc (d) passe par le point B ( 0;-3)
III) Lire graphiquement le coefficient directeur et l’ordonnée à l’origine d’une droite
Exercice résolu:
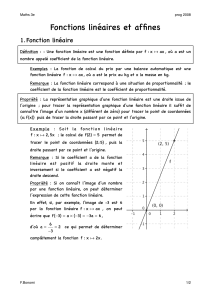
Dans le repère ci-dessous, sont représentées deux droites (d1) et (d2). La droite (d1) est la représentation
graphique d’une fonction affine f et la droite (d2) celle d’une fonction affine g.
1. Lire graphiquement les coefficients directeurs et les ordonnées à l’origine des droites (d1) et (d2).
2. En déduire les expressions algébriques des fonctions affines f et g.
1)
2) La droite (d1) la représentation graphique de la fonction affine f définie par : f(x)=3x+4.
La droite (d2) est la représentation graphique de la fonction affine g définie par : g(x) = - 0,5x+2.

IV) Proportionnalité des accroissements :
Propriété (admise) : Soit f une fonction affine définie par
!
f:xaax +b
où a et b sont deux nombres fixés
Si x1 et x2 sont deux nombres distincts alors :
!
a=f(x1)"f(x2)
x1"x2
=écart des f(x)
écart des x
Autrement dit : Les accroissements de f(x) sont proportionnels aux accroissements de x et le coefficient de
proportionnalité est a .
V) Déterminer une fonction affine à partir de deux nombres et de leurs images.
Exercice résolu : Soit f une fonction affine telle que f(4) = 22 et f(-6) = -38 .
Déterminer l’expression algébrique de la fonction f.
Première façon : En utilisant la proportionnalité des accroissements :
• f est une fonction affine donc son expression algébrique est de la forme : f(x) = ax+b où a et b sont les
coefficients à déterminer.
Calcul de a :
Si x 1
!
"
x2 alors
!
a=f(x1)"f(x2)
x1"x2
!
a=f(4) "f("6)
4"("6)
a=22 "("38)
10
a=60
10
a=6
Calcul de b :
On sait que f(4) =22 et que f(x) = 6x+ b
D’où :
!
6"4+b=22
24 +b=22
b=22 #24
b=#2
Conclusion : L’expression algébrique de f est :
!
f(x)=6x"2
Deuxième façon : En résolvant un système de deux équations à deux inconnues: