3ème - Euler

3ème D
Idées de correction du contrôle de Math. 11
Exercice 1
Pour chacune des phrases suivantes, entourer la (ou les) bonne(s) réponse(s).
A
B
C
D
La fonction est une fonction
affine
14 xx
7
3
x
x
15 2xx 
xx 5,0
La fonction est une fonction
linéaire
0x
xx 9
3xx 
1x
L'image du nombre
3
par la
fonction
xxg 6: 
est :
3
)3(g
)6(g
18
L'antécédent du nombre -5 par la
fonction
36:  xxh 
est :
)5(h
33
1,3
3
4
Exercice 2
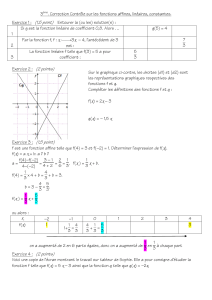
La courbe ci-contre est la courbe représentative de la
fonction f définie par
56: 2 xxxf 
.
1. a)
325969)9( 2f
L’image de 9 par la fonction f est égale à 32.
605)5(6)5()5( 2f
L’image de -5 par la fonction f est égale à 60.
b) Vérifier ces résultats sur la courbe en faisant
apparaître des pointillés (en rouge)
2. Graphiquement, déterminer le (les) antécédents
de 20 par la fonction f (en bleu).
Graphiquement, les antécédents le 20 par la
fonction f sont -1,9 et 7,9.
Exercice 3
1. Soit f la fonction linéaire définie par
xxf 5: 
.
On cherche un nombre x tel que
4)( xf
, c'est-à-dire
45  x
, donc
5
4
x
.
L’antécédent du nombre 4 par la fonction f est égal à
5
4
.
2. Soit h une fonction linéaire telle que
5,7)4( h
.
On sait que h est une fonction linéaire, h s’écrit donc sous la forme
axxh :
où a est un nombre
fixé.
On a donc
)4()4(
5,7)4(
ah
h
donc
5,7)4( a
et
875,1)4(5,7 a
La fonction h est donc définie par
xxh 875,1: 

Exercice 4
1. Soit g la fonction affine définie par
76: xxg 
.
7706)0( g
L’image de 0 par la fonction g est égale à -7.
2075,46)5,4( g
L’image de 4,5 par la fonction g est égale à 20.
2. Soit f la fonction affine vérifiant
7)2( f
et
18)3( f
.
On sait que le fonction f est une fonction affine, f s’écrit donc sous la forme
baxxf :
, où a et
b sont deux nombres fixés.
Calcul de a
On sait que
5
5
25
)3(2 )18(7 )3(2 )3()2( 
ff a
Donc f s’écrit sous le forme
bxxf 5: 
Calcul de b
On a donc
bbf
f
1025)2(
7)2(
donc
710 b
et
3107b
.
La fonction f est donc définie par
35: xxf 