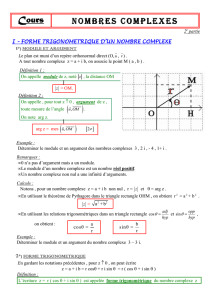
F025 Forme trigonométrique des nombres complexes

Forme trigonométrique d'un nombre complexe
Si z = x + iy , alors |z| = z. z = x² + y²
|z| = 0 équivaut à z = 0
|z + z'| ≤ |z| + |z'| ; |− z| = |z| ; |−z| = |z| ; |zz'| = |z||z'| ; |z
n
| = |z|
n
1
z = 1
|z| ; 
z
z' = |z|
|z'|
Si z = x + iy , alors arg(z) = θ (2π) avec
cos θ = x
x² + y²
sin θ = y
x² + y²
z réel non nul équivaut à arg(z) = 0 ou π (2π)
z imaginaire pur non nul équivaut à arg(z) = π
2 ou arg(z) = − π 2
arg(− z) = − arg(z) ; arg(−z) = arg(z) + π
arg(zz') = arg(z) + arg(z') ; arg(z
n
) = n arg(z)
arg 
1
z = − arg (z) ; arg 
z
z' = arg (z) − arg(z')
L'écriture z = |z|(cos θ + i sin θ) est la forme trigonométrique de z
z = z' ⇔ |z| = |z'| et arg(z) = arg(z') (2π)
|z| = ρ et arg(z) = α (2π) ⇔ z = ρ(cos α + i sin α) avec ρ > 0
§ z et z' sont deux nombres complexes tels que : zz' ≠ − 1 et |z| = |z'| = 1
Démontrer que le nombre z + z'
1 + zz' est un nombre réel
§ a. Déterminer le module et un argument du complexe z = 6 + i 2 .
b. En déduire la forme trigonométrique de z .
§ 1. a. Pourquoi l'écriture z = − 2(cos π
6 + i sin π 6) n'est pas la forme trigonométrique de z ?
b. Ecrire z sous forme trigonométrique
2. Reprendre la question 1. avec le nombre complexe z = 2 (cos π
4 − i sin π 4)
3. Donner la forme trigonométrique de z = sin α + i cos α
§ Ecrire sous forme trigonométrique le complexe (1 + i)²
(1 − i)
3
. En déduire sa forme algébrique
§ a. écrire 1 + i 3
1 + i sous forme algébrique, puis trigonométrique .
b. En déduire les valeurs exactes de cos
π
12 et sin
π
12 .