Le pendule pesant

Le pendule pesant
par Gilbert Gastebois
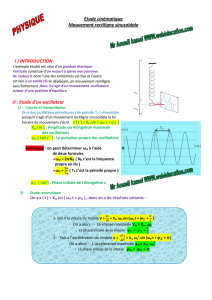
1. Schéma
L0 Longueur du pendule = distance entre
l'axe et le centre de gravité du pendule.
m Masse du pendule
J
Moment d'inertie du pendule par rapport à
son axe. Pour un pendule simple J = mL0²
mg Poids du pendule
R Réaction de l'axe
f
Force de frottement fluide sur le pendule
2. Etude du mouvement du pendule pesant
2.1 Équation différentielle du mouvement.
Équation de Newton : J d²θ/dt² = Σ MF
J d²θ/dt² = Mmg + Mf + MR
J d²θ/dt² = - mg L0 sinθ - f L0 + 0
f = - k v = - k L0 ω = - k L0 dθ/dt ( frottement fluide laminaire )
J d²θ/dt² = - mg L0 sinθ - k L02 ω = - mg L0 sinθ - k L02 dθ/dt
d²θ/dt² = - k L02/J dθ/dt - mg L0/J sinθ
On pose mg L0/J = ω02 et k L02/J = γ
d²θ/dt² + γ dθ/dt + ω02 sinθ = 0
2.2 Équation différentielle pour les petits angles.
Cette équation n'a pas de solution analytique, sa solution est numérique. Cependant, on peut
la traiter dans l'approximation des petits angles.
θ petit => sinθ = θ
on a alors :
d²θ/dt² + γ dθ/dt + ω02 θ = 0
Solution de l'équation : Cliquer ici
3. Etude du pendule sans frottement
3.1 Équation différentielle pour les petits angles.
Si γ = 0, alors d²θ/dt² + ω02 θ = 0
donc θ = θm sin ( ω0 t + φ )
dθ/dt = θmω0 cos ( ω0 t + φ )
Conditions initiales : A t = 0 θ = θ0 et
θ0 = θm sinφ et θ '0 = θm ω0 cosφ
tan φ = ω0 θ0/θ'0 et θm = θ0/arctanφ
dθ/dt = θ'0
3.2 Période du mouvement pour les petits angles.
T0 = 2π/ω0 = 2π( J/mgL0 )1/2
T0 = 2π( J/mgL0 )1/2
Pour un pendule simple J = mL02 donc T0 = 2π( L0/g )1/2
3.3 Étude énergétique
Sans frottement, Em = constante ( On pose dθ/dt = θ'
)
Em = Ec + Ep = 1/2 Jθ'2 + mgz = 1/2 Jθ'2 + mg( L0 - L0 cosθ ) = 1/2 Jθ'2 + mgL0 (1 - cosθ )
Em = 1/2 Jθ'2 + mgL0 (1 - cosθ )
A θ = θm , θ' = 0 donc Em = mgL0 (1 - cosθm )
mgL0 (1 - cos θm ) = 1/2 Jθ'2 + mgL0 (1 - cosθ )
mgL0 cos θm = -1/2 Jθ'2 + mgL0 cosθ
θ'2 = 2 mgL0/J( cos θ - cosθm )
θ' = (2 mgL0/J( cosθ - cosθm ))1/2 = (2 ω02 ( cosθ - cosθm ))1/2
Remarque : En dérivant , on retrouve l'équation différentielle du mouvement
θ' = (2 ω02 ( cosθ - cosθm ))1/2
d²θ/dt² = 1/2 (2 ω02 ( cosθ - cosθm ))-1/2( - 2 ω02 sinθ θ' ) =
- ω02 sin θ θ' /(2 ω02 ( cosθ - cosθm ))1/2
Comme θ' = (2 ω02 ( cosθ - cosθm ))1/2, l'expression se simplifie, il reste
d²θ/dt² = - ω02 sinθ
d²θ/dt² + ω02 sinθ = 0
On peut aussi utiliser le Lagrangien :
L = Ec - Ep = 1/2 Jθ'2 - mgL0 (1 - cosθ )
Formule de Lagrange : d(dL/dθ')/dt - dL/dθ = 0
Jd²θ/dt² + mgL0 sinθ = 0 et
d²θ/dt² + ω02 sinθ = 0
4. Etude du mouvement sans frottement pour les grands angles
4.1 Formule de Borda pour les angles moyens.
d²θ/dt² = - ω02 sinθ
On développe sinθ en décomposition de Taylor sinθ = θ - θ3/6 + θ5/120 + ....
d²θ/dt² = - ω02 ( θ - θ3/6 + θ5/120 + .... )
On prend θ = θm sin(ω t) avec ω = ω0 ( 1- ε )
( ε petit )
- ω2θm sin(ω t) = - ω02 ( θm sin(ω t) - 1/6 θm3 sin3(ω t)) On se limite aux deux premiers
termes.
- ω02 (1 - 2ε ) θm sin(ω t) = - ω02( θm sin(ω t) - 1/6 θm3 sin3(ω t))
sin3ω t = 3/4 sin(ω t) - 1/4 sin(3 ω t) ( d'après sin(ω t) = ( eiωt - e-iωt ) /2i )
- ω02 (1 - 2ε ) θm sin(ω t) = - ω02( θm sin(ω t) - 1/6 θm3 (3/4 sin(ω t) - 1/4 sin(3ω t)))
On obtient :
2 ε θm sin(ω t) = 1/8 θm3 sin(ω t) - 1/24 θm3 sin(3ω t) = f(t)
f(t) est une fonction périodique de pulsation fondamentale ω avec une harmonique de rang 3.
Comme on s'intéresse seulement à la période fondamentale, on peut abandonner le terme
harmonique qui modifie la forme de f(t), mais pas sa période. On remplace ainsi f(t) par son
fondamental : f(t) = 1/8 θm3 sin(ω t). On a donc :
2 ε θm sin(ω t) = 1/8 θm3 sin(ω t)
ε = θm2 /16 donc
ω = ω0 (1 - θm2 /16)
θm2 /16 << 1, ce qui fait θm << 4 rd ou θm << 240°. En
pratique, on peut prendre θm < 60°
T = 2π/ω = 2π/(ω0 (1 - θm2/16)) = 2π/ω0 (1 + θm2/16) = T0 (1 + θm2/16)
T = T0 (1 + θm2/16)
Cette formule est valable avec une remarquable précision jusqu'à θm = 60 °.
T = T0 (1 + θm2/16)
pour des angles inférieurs à 60°
4.2 Formule générale de la période.
D'après la conservation de l'énergie ( Cf 3.3 ), on a :
θ' = (2 mgL0/J( cosθ - cosθm ))1/2 = (2 ω02 ( cosθ - cosθm ))1/2 or
donc
θ' = dθ/dt donc dt = dθ/θ' = dθ/(2 ω02 ( cosθ - cosθm ))1/2 =
cosθ = 1 - 2 sin2(θ/2)
dθ/(2 ω02 (1 - 2sin²(θ/2) - 1 + 2 sin²(θm/2)1/2
dt = dθ/(4 ω02 (sin²(θm/2) - sin²(θ/2))1/2
On pose u = sin(θ/2)/sin(θm/2) et k = sin(θm/2)
sin²(θ/2))1/2 dθ
d'où
u = sin(θ/2)/k
donc du = 1/2 cos(θ/2)/k dθ = (1 /(2k) = (1 - k²u²)1/2 dθ /(2k) donc
dθ = 2k du/(1 - k²u²)1/2
dt = 2k du/((1 - k²u²)(4 ω02 (k² - k²u²)))1/2 = 2k du/((1 - k²u²)(4 k² ω0² (1 - u²)))1/2 =
du /ω0 /((1 - k²u²)(1 - u²))1/2
dt = du /ω0 /((1 - k²u²)(1 - u²))1/2
Si on intègre dt de θ = 0 à θ = θm, ce qui correspond à u = 1, on obtient le quart de la
période donc
T = 4/ω0
du / ((1 - k²u²)(1 - u²))1/2 = 4/ω0 K(k) = 2 T0/π K(sin(θm/2))
K(k) est l'intégrale elliptique de Legendre:
K(k) = π/2 (1 + k2/4 + 9/64 k4 + .... + ((2n)!/(2n n!)2)2 k2n +...) = π/2 Σ ((2n)!/(2n n!)2)2 k2n
T = T0 (1 + 1/4 sin2(θm/2) + 9/64 sin4(θm/2) + 25/256 sin6(θm/2) + .... +
((2n)!/(2n n!)2)2 sin2n(θm/2) + .... )
T = T0 Σ((2n)!/(2n n!)2)2 sin2n(θm/2)
Si on prend les deux premiers termes pour θm assez petit pour qu'on puisse remplacer sin
θm/2 par θm/2 , on obtient :
T = T0 ( 1 + θm2/16 )
On obtient :
On retrouve la formule de Borda
θm °
0 10
1+ θm2/16
(en rd)
1 1,00 1,01 1,02 1,03 1,05 1,07 1,09 1,12 1,15 1,19 1,23 1,27 1,32 1,37 1,43 1,49 1,55 1,62
20
30
40
50
60
70
80
90 100 110 120 130 140 150 160 170 180
2/π
K(sin(θm/2)) 1 1,00 1,01 1,02 1,03 1,05 1,07 1,10 1,14 1,18 1,23 1,29 1,37 1,47 1,59 1,76 2,01 2,44 infini
Si on prend les trois premiers termes :
T = T0 ( 1 + sin2(θm/2)/4 + 9/64 sin4(θm/2) + 25/256 sin6(θm/2) )
sin2(θm/2) = ( θm/2 - θm3/48)2 = θm2/4 - θm4/48 + θm6/1440
sin4(θm/2) = θm4/16 - θm6/96
sin6(θm/2) = θm6/64
( on se limite à la puissance 6 )
( on se limite encore à la puissance 6 )
( on se limite toujours à la puissance 6 )
1 + sin2(θm/2)/4 + 9/64 sin4(θm/2) + 25/64 sin6(θm/2) = 1 + θm2/16 - θm4/192 + 9/1024 θm49/6144 θm6 + 1/5760 θm6 + 25/16384 θm6 = 1 + θm2/16 + 11/3072 θm4 + 173/737280 θm6
T = T0 ( 1 + 1/16 θm2 + 11/3072 θm4 + 173/737280 θm6 )
jusqu'à θm = 140 °)
( approximation assez précise
4.3 Équation horaire θ = f(t).
Le mouvement général du pendule est périodique donc f(t) peut être écrit sous forme d'une
série de Fourier :
θ = a1 cos(ωt) + a2 cos(2ωt) + a3 cos(3ωt) + ..... + b1 sin(ωt) + b2 sin(2ωt) + b3 sin(3ωt) + .....
Le mouvement du pendule est le même pour θ > 0 et θ <0 et symétrique pour la montée et
pour la descente.
On prend des conditions initiales telles que à t = 0, f'(t) = 0. Dans ces conditions, les
coefficients des cosinus et ceux des harmoniques paires sont tous nuls.
Il reste θ = b1 sin(ωt) + b3 sin(3ωt) + b5 sin(5ωt) +.... L'oscillation étant proche d'un sinus, il
est probable que les coefficients bn sont faibles par rapport à b1 et qu'ils décroissent très vite,
on ne conserve donc que le premier harmonique. On pose donc :
θ = a sin(ωt) + b sin(3ωt)
L'équation différentielle est :
d²θ/dt² = - ω02 sinθ
On développe sinθ en décomposition de Taylor sinθ = θ - θ3/6 + θ5/120 + .... On ne garde
que les deux premiers termes
d²θ/dt² = - ω02 ( θ - θ3/6 + θ5/120 ) On remplace θ par a sin(ωt) + b sin(3ωt)
- a ω² sin(ωt) - 9bω² sin(3ωt) = a sin(ωt) + b sin(3ωt) - 1/6 ( a sin(ωt) + b sin(3ωt))3 - 1/120
( a sin(ωt) + b sin(3ωt))5
On néglige les termes de puissance supérieure à a5
- a ω² sin(ωt) - 9bω² sin(3ωt) = a sin(ωt) + b sin(3ωt) - 1/6 ( a3 sin3(ωt) + 3a2b
sin2(ωt)sin(3ωt)) - 1/120 a5 sin5(ωt)
On développe et on linéarise par la formule d'Euler ( sinθ = (eiθ - e-iθ)/2i )
sin3θ = 3/4 sinθ -1/4 sin(3θ)
sin2θ sin(3θ) = -1/4 sinθ + 1/2 sin(3θ) -1/4 sin(5θ)
sin2(3θ) sinθ = 1/2 sinθ +1/4 sin(5θ) -1/4 sin(7θ)
sin5θ = 5/8 sinθ - 5/16 sin(3θ) + 1/16 sin(5θ)
- a ω² sin(ωt) - 9bω² sin(3ωt) = - ω0²((a - 3a3/24 + 3a2b/24 + 5a5/8) sin(ωt) + (b - 6a2b/24 +
a3/24) sin(3ωt))
Il faut (a - 3a3/24 + 3a2b/24 + a5/192)/a = (b - 6a2b/24 + a3/24)/(9b)
216b - 27a2b + 27ab2 + 9a4b/192 = 24b - 6a2b + a3
192b - 21a2b + 27ab2 + 9a4b/192 = a3
On néglige ab2 et a4b, on obtient : b = a3/(192 - 21a2). Si a << 3, on obtient
b = a3/192 (1 + 21/192 a2) = a3/192 donc :
θ = a sin(ωt) + a3/192 sin(3ωt)
Remarque :
Si on préfère des conditions initiales où θ = θm, on aura ωt remplacé par ωt + π/2 et
θ = a cos(ωt) - a3/192 cos(3ωt)
Amplitude maximale :
On a l'amplitude maximale pour ωt = π/2 donc
θm = a - a3/192
Il n'est pas facile d'en déduire a = f(θm), les équations du troisième degré sont pénibles, mais
a est proche de θm, donc on pose : a = θm(1 + ε) et on se limite au premier ordre en ε
θm = θm(1 + ε) - θm3(1 + 3 ε )/192 = θm + ε θm - θm3/192 - 3 ε θm3/192
ε (1 - 3 θm2/192 ) = θm2/192
ε = θm2/192 /(1 - 3 θm2/192 ) ≃ θm2/192
car
3 θm2/192 << 1
a = θm + θm3/192
Période du mouvement :
On a : a ω² = ω0²(a - 3a3/24 + 3a2b/24 + a5/192) avec b = a3/192 donc
ω² = ω0²(1 - a2/8 + a4/1536 + a4/192) = ω0²(1 - a2/8 + 9a4/1536 )
On a ( 1 + ε ) 1/2 = 1 + 1/2 ε - 1/8 ε2 donc (1 - a2/8 + 9a4/1536)1/2 = 1 - a2/16 +
9a4/3072 - a4/512 = 1 - a2/16 + 3a4/3072
ω = ω0(1 - a2/16 + a4/1024 ) ou en remplaçant a par θm + θm3/192
ω = ω0(1 - θm2/16 + θm4/3072)
Formules précises jusqu'à a = 2,3 ( θm = 130 ° )
T = 2π/ω = 2π/(ω0(1 - θm2/16 + θm4/3072)) = T0 (1 - θm2/16 + θm4/3072)) -1
On a ( 1 + ε ) -1 = 1 - ε + ε2
donc (1 - θm2/16 + θm4/3072)-1 = 1 + θm2/16 - θm4/3072 +
θm4/256 = 1 + θm2/16 + 11/3072 θm4
T =T0 (1 + θm2/16 + 11/3072 θm4)
de Legendre de la période.
On retrouve les trois premiers termes de la formule
Pour θm < 2,5 rd ( 140 ° )
θ = ( θm + θm3/192) sin( ωt) + θm3/192 sin(3ωt)
ω = ω0(1 - 1/16 θm2 + 1/3072 θm4 - 23/737280 θm6)
5. Cas de la rotation du pendule sans frottement.
5.1 Vitesse angulaire maximale indispensable.
Si la vitesse angulaire maximale dépasse une certaine valeur, le pendule n'oscille plus, il
tourne autour de son axe.
Cela arrive quand la vitesse ne s'annule jamais, donc quand la vitesse θmin en haut de la
trajectoire ( z = 2 L0 ) est supérieure à zéro.
On a alors 1/2 Jθ'm2 = 1/2 Jθ'min2 + 2 mgL0 > 2 mgL0 donc θ'm2 > 4 mgL0/J
ou
θ'm > 2 ω0
Remarque : Pour un pendule simple constitué d'une boule reliée à un fil, il faut que le fil
reste tendu donc il faut qu'en haut de la trajectoire, la tension du fil soit positive donc il faut
que
ml θmin2 > mg donc θmin > (g/L0)1/2 ou θmin > ω0
donc Em = 1/2 mL0²θ'm2 > 2 mgL0 + 1/2 mL0²θ'min2 donc θ'm2 > 4 mg/L0 + mL0²θ'min2
θ'm2 > 4 mg/L0 + mg/L0 donc θ'm > ( 5 mg/L0 )1/2
5.2 Période de rotation.
D'après la conservation de l'énergie ( Cf 3.3 ), on a :
Em = 1/2 Jθ'2 - mgL0 ( 1 - cosθ ) = 1/2 Jθ'm2
θ'² = θ'm2 - 2 mgL0/J( 1 - cosθ )
or
1 - cosθ = 2 sin2(θ/2) donc
θ' = ( θ'm2 - 2 ω02 ( 1 - cosθ ))1/2 = ( θ'm2 - 4 ω02 sin2(θ/2) )1/2
θ' = dθ/dt donc dt = dθ/θ' = dθ/( θ'm2 - 4 ω02 sin2(θ/2) )1/2
dt = dθ/( θ'm2 - 4 ω02 sin2(θ/2) )1/2
On pose u = sin(θ/2)
donc du = 1/2 cos(θ/2) dθ = 1/2 dθ (1 - sin2(θ/2))1/2 = 1/2 dθ (1 - u2)1/2 donc
dθ = 2 du/(1 - u2)1/2
dt = 2 du/((1 - u2)( θ'm2 - 4 ω02 sin2(θ/2) ))1/2 = 2/θ'm du/((1 - u2)(1 - 4 ω02/θ'm2 u2)))1/2 =
2/θ'm /((1 - u2)(1 - k2 u2))1/2 du
en posant k = 2 ω0/θ'm = θ'0/θ'm
( θ'0 = 2 ω0 est la valeur minimale de θ'm
permettant au pendule de tourner autour de son axe )
dt = 2/θ'm /((1 - u2)(1 - k2u2))1/2 du
Si on intègre dt de θ = 0 à θ = π, ce qui correspond à u = 1, on obtient la moitié de la
période donc
T = 4/θ'm
du / ((1 - u²)(1 - k² u²))1/2 = 4/θ'm K(k) = 4/θ'm K(θ'0/θ'm )
K(k) est l'intégrale elliptique de Legendre :
K(k) = π/2 (1 + k2/4 + 9/64 k4+ .... + ((2n)!/(2n n!)2)2 k2n +... ) = π/2 Σ ((2n)!/(2n n!)2)2 k2n
T = 2π/θ'm (1 + 1/4 (θ'0/θ'm )2 + 9/64 (θ'0/θ'm )4 + 25/256 (θ'0/θ'm )6 + .... +
((2n)!/(2n n!)2)2 (θ'0/θ'm )2n + .... )
T = 2π/θ'm Σ ((2n)!/(2n n!)2)2 (θ'0/θ'm )2n
Par exemple en prenant L0 = 1 m, θ'0 = 6,264 rd/s, on a alors :
θ'm /θ'0
1
T (s)
1,001 1,005 1,02
1,05 1,118
infini 2,878 2,353 1,898 1,589 1,289
1,3
1,45
0,953
1,6
1,75
1,9
2,1
2,135
0,808 0,707 0,631 0,572 0,509 0,500
Si θ'm >> θ'0, K(k) tend vers K(0) = π/2 et T tend vers Tf = 2π/θ'm ( θ'm est quasiconstante, le poids n'influe presque plus sur le mouvement et on a un mouvement circulaire
quasi-uniforme )
Si on prend les quatre premiers termes :
T = 2π/θ'm (1 + 1/4 (θ'0/θ'm )2 + 9/64 (θ'0/θ'm )4 + 25/256(θ'0/θ'm )6 )
( On obtient T avec une très bonne précision pour θ'm > 1,5 θ'0 )
Remarque : Pour le pendule simple avec un fil, il faut que θ'm /θ'0 = (5/4)1/2 ce qui donne
θ'm /θ'0 = 1,118.
La période maximale de rotation d'un pendule de 1m, permettant au fil de rester tendu est
alors de 1,289 s.
Intégrale elliptique de Legendre K(x)
K(x), l'intégrale elliptique de Legendre est définie, pour 0 <= | x | <1, par :
K (x) =
du / ((1 - u²)(1 - x²u²))1/2
Sa valeur est donnée par la série suivante :
K(x) = π/2 (1 + 1/4 x2 + 9/64 x4 + 25/256 x6 + .... + ((2n)!/(2n n!)2)2 x2n + ... )
K(x) = π/2 Σ((2n)!/(2n n!)2)2 x2n
n! est la factorielle de n
On obtient :
x
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
( La somme allant de 0 à l'infini )
0,8
0,9
0,95 0,975 0,987 0,993 0,996 0,998 0,999
1
2/π K(x) 1 1,003 1,010 1,024 1,044 1,073 1,115 1,175 1,270 1,452 1,649 1,855 2,056 2,248 2,424 2,642 2,862 infini
Remarque : si x = 0, l'intégrale est directement calculable, elle donne
arcsin(1) - arcsin(0) =π/2, ce qu'on retrouve en calculant la série.