Interrogation no 3 Sujet 1 Exercice 1 (cours, 4 points) 1. Soit (un

Interrogation no3
Sujet 1
Exercice 1 (cours, 4 points)
1. Soit (un) une suite r´eelle d´efinie sur N. Donner la d´efinition
du fait que (un) est major´ee.
2. Soit fune fonction d´efinie sur un intervalle I. Soit a∈I.
Donner la d´efinition du fait que fest d´erivable en a.
3. Donner l’expression de la fonction d´eriv´ee des fonctions sui-
vantes.
(a) Pour tout x∈R,f(x) = x
(b) Pour tout x∈R,g(x) = x3.
(c) Pour tout x6= 0, h(x) = 1
x.
Exercice 2 (5 points)
Les questions 1 et 2 sont ind´ependantes.
1. Soit (Vn) la suite d´efinie pour tout n∈Npar Vn= 8 −n2.
(a) Calculer V0,V1et V2.
(b) ´ Etudier les variations de (Vn).
2. Soit (un) la suite d´efinie par u0= 3 et pour tout n∈N,
un+1 =un−n2+ 3.
(a) Calculer u1et u2.
(b) ´ Etudier les variations de (un).
Exercice 3 (4,5 points)
On consid`ere la suite (An) d´efinie par A0= 1 et pour tout entier
n>0, An+1 =1
3An+ 4.
1. Calculer A1et A2(r´ediger les calculs).
2. Utiliser la calculatrice pour donner une valeur approch´ee de
A8. Arrondir `a 10−4pr`es.
3. On admet que la suite (An) converge vers 6.
(a) ´ Ecrire un algorithme qui renvoie le plus petit entier n0
tel que |An0−6|<10−7.
(b) Programmer l’algorithme `a la calculatrice et indiquer la
valeur de n0.
Exercice 4 (1 point)
Donner un exemple de suite croissante et born´ee (la suite pourra
ˆetre d´efinie par son terme g´en´eral ou par r´ecurrence). Aucune jus-
tification n’est attendue.
Exercice 5 (4 points)
Soit fla fonction d´efinie sur Rpar f(x) = x2−5x
1. En revenant `a la d´efinition, ´etudier la d´erivabilit´e de fen
2, et montrer que f′(2) = −1.
2. En d´eduire une ´equation de la tangente `a la courbe
repr´esentative de fau point d’abscisse 2.
Exercice 6 (1,5 points)
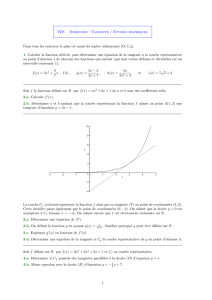
On a trac´e ci-contre la courbe repr´esentative d’une fonction f
d´efinie et d´erivable sur R. La droite T1est tangente `a la courbe en
A, et la courbe admet une tangente parall`ele `a l’axe des abscisses
au point B.
1. D´eterminer f′(−3). Justifier.
2. D´eterminer f′(1). Justifier.
−1
−2
−3
−4
−5
−6
−7
1
2
123456−1−2−3−4−5
A
B
T1
Exercice 7 (bonus, 1 point)
Montrer que la courbe de la fonction inverse admet en deux points
une tangente parall`ele `a la droite d’´equation y=−1
4x+ 3 et
pr´eciser les abscisses de ces deux points.

Interrogation no3
Sujet 2
Exercice 8 (cours, 4 points)
1. Soit (un) une suite r´eelle d´efinie sur N. Donner la d´efinition
du fait que (un) est d´ecroissante.
2. Soit fune fonction d´efinie sur un intervalle I. Soit a∈I.
Donner la d´efinition du fait que fest d´erivable en a.
3. Donner l’expression de la fonction d´eriv´ee des fonctions sui-
vantes.
(a) Pour tout x∈R,f(x) = x2
(b) Pour tout x > 0, g(x) = √x.
(c) Pour tout x∈R,h(x) = k(fonction constante).
Exercice 9 (5 points)
Les questions 1 et 2 sont ind´ependantes.
1. Soit (Vn) la suite d´efinie pour tout n∈Npar Vn=−2
n+ 1.
(a) Calculer V0,V1et V2.
(b) ´ Etudier les variations de (Vn).
2. Soit (un) la suite d´efinie par u0= 3 et pour tout n∈N,
un+1 =un+ 3n+ 1.
(a) Calculer u1et u2.
(b) ´ Etudier les variations de (un).
Exercice 10 (4,5 points)
On consid`ere la suite (An) d´efinie par A0= 1 et pour tout entier
n>0, An+1 =3
2An+ 1.
1. Calculer A1et A2(r´ediger les calculs).
2. Utiliser la calculatrice pour donner une valeur approch´ee de
A8. Arrondir `a 10−4pr`es.
3. On admet que la suite (An) diverge vers +∞.
(a) ´ Ecrire un algorithme qui renvoie le plus petit entier n0
tel que An0>105.
(b) Programmer l’algorithme `a la calculatrice et indiquer la
valeur de n0.
Exercice 11 (1 point)
Donner un exemple de suite croissante et minor´ee par 5 (la suite
pourra ˆetre d´efinie par son terme g´en´eral ou par r´ecurrence). Au-
cune justification n’est attendue.
Exercice 12 (4 points)
Soit fla fonction d´efinie sur Rpar f(x) = 3x2+x
1. En revenant `a la d´efinition, ´etudier la d´erivabilit´e de fen
−1, et montrer que f′(−1) = −5.
2. En d´eduire une ´equation de la tangente `a la courbe
repr´esentative de fau point d’abscisse −1.
Exercice 13 (1,5 points)
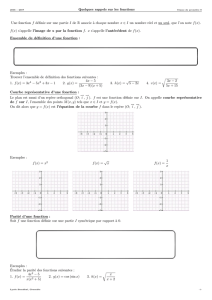
On a trac´e ci-contre la courbe repr´esentative d’une fonction f
d´efinie et d´erivable sur R, et les tangentes `a cette courbe aux points
Aet B.
1. D´eterminer f′(−4). Justifier.
2. D´eterminer f′(−1). Justifier.
−1
−2
1
−1−2−3−4−5
c
A
B
Exercice 14 (bonus, 1 point)
Montrer que la courbe de la fonction inverse admet en deux points
une tangente parall`ele `a la droite d’´equation y=−1
4x+ 3 et
pr´eciser les abscisses de ces deux points.