cours 1

1 Limites de fonctions
1.1 limites en l’in…ni
1.1.1 Limites in…nies en l’in…ni
Dé…nition 1 Soit fune fonction.
On dit que f(x)a pour limite +1lorsque xtend vers +1( respectivement 1) si et seulement si :
pour tout nombre A(A2R), tous les nombres f(x)sont plus grands dès que xest assez grand (respectivement
xassez grand)
Dé…nition 2 Énoncés analogues pour une limite égale à 1
Exemple 3 des limites à connaitre
lim
x!+1px= +1
lim
x!+1xn= +1pout tout n2N
lim
x!1 xn=1 pour tout n2Nimpair
lim
x!1 xn= +1pour tout n2Npair
1.1.2 Limite …nie en l’in…ni
Dé…nition 4 limite `
Soit `un nombre réel. On dit que la fonction fa pour limite `quand xtend vers +1(respectivement
1)si et seulement si : pour tout intervalle ouvert Icentré sur `, les nombres f(x)sont tous dans Idès que
xest assez grand (respectivement xassez grand). On note :
lim
x!+1f(x) = `(Respectivement : lim x!1 f(x) = `)
Dé…nition 5 On dira alors que la droite d’équation y=`est asymptote horizontale à la courbe représenta-
tive de f(en +1ou 1 selon le cas.)
Propriété 6 Soit fune fonction dé…nie sur un intervalle Ide la forme ]A; +1[. S’il existe deux réels aet b
tels que f(x) = ax +b+g(x)avec lim
x!+1g(x) = 0 alors la droite d’équation y=ax +best une asymptote
oblique à la courbe de fau voisinage de +1.
Exemple 7 Soit f(x) = 2x+x22
x
Trouvons trois nombres a,bet ctels que f(x) = ax +b+c
x.
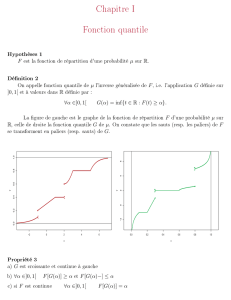
La courbe de f:x7! x2 + 2
x

-5 -4 -3 -2 -1 1 2 3 4 5
-7
-6
-5
-4
-3
-2
-1
1
2
3
x
y
admet une asymptote oblique d’équation y=x2au voisinage de +1et au voisinage de 1.
Exercise 1 Soit fla fonction dé…nie par :
f(x) = x3+ 2x2x+ 3
x2+ 1
1. Déterminer trois réels a,bet ctels que f(x) = ax +b+c
x2+ 1.
2. Calculer la limite de f(x)(ax +b)en +1puis en 1.
3. En déduire que la courbe représentative de f,Cadmet une asymptote oblique en 1 et en +1.
4. Étudier les positions relatives de Cet de .
1.2 limite d’une fonction lorsque la variable tend vers un réel a
fest une fonction dé…nie sur un intervalle Icontenant aou dont aest une borne. (fpeut ne pas être dé…nie
en a)
1.2.1 limite …nie en a
Dé…nition 8 Limite `en a
On dit que ftend vers `quand xtend vers asi et seulement si :
pour tout intervalle ouvert Jcontenant `, tous les nombres f(x)appartiennent à Jdès que x2Iest assez
proche de a
1.2.2 Limite in…nie en a
Dé…nition 9 On dit que ftend vers +1(respectivement 1) lorsque xtend vers asi et seulement si :
pour tout intervalle J=]; +1[( respectivement ]1;[)2R, tous les nombres f(x)appartiennent à J
dès que x2Iest assez proche de a.
Dé…nition 10 Lorsque l’on a :
lim
x!af(x) = 1
on dira que la droite d’équation x=aest asymptote verticale à la courbe de f.

Exemple 11 L’hyperbole d’équation y=1
x+ 2 admet une asymptote d’équation x=2.
-5 -4 -3 -2 -1 1 2 3 4 5
-5
-4
-3
-2
-1
1
2
3
4
5
x
y
1.3 Opérations sur les limites
Dans tous les tableaux qui suivent, désigne un réel, ou +1, ou 1 et `et `0désignent deux réels.
Les fonctions fet gconsidérées sont dé…nies au voisinage de .
Les limites de ces fonctions sont déterminées en .
1.3.1 limite d’une somme
Si fa pour limite ` ` ` +1 1 +1
Si ga pour limite `0+1 1 +1 1 1
f+ga pour limite `+`0+1 1 +1 1 ?
1.3.2 limite d’un produit
Si fa pour limite ` ` > 0` > 0` < 0` < 0 +1+1 1 0
Si ga pour limite `0+1 1 +1 1 +1 1 1 1
fga pour limite ` ` 0+1 1 1 +1+1 1 +1?
Exemple 12 Déterminer la limite en 1 de la fonction fdé…nie sur Rpar : f(x) = x31
x2.
limx!1 1
x2=2
limx!1 x3=1 9
=
;limx!1 f(x) = +1.
limite en l’in…ni d’une fonction polynôme
Déterminer limx!+12x44x2+ 16
Méthode 13 La limite en 1 d’un polynôme est égale à la limite en 1 de son monôme de plus haut degré.

1.3.3 limite d’un quotient
cas où le dénominateur a une limite non nulle
Si fa pour limite ` ` +1+1 1 1 1
Si ga pour limite `06= 0 1 `0>0`0<0`0>0`0<01
f
ga pour limite ` `00+1 1 1 +1?
cas où le dénominateur a une limite nulle
fa pour limite ` > 0` > 0` < 0` < 00
ga pour limite 0+00+00
f
ga pour limite +1 1 1 +1?
Soit fla fonction dé…nie sur Rn1
2par : f(x) = x2 4x2.
limx!1
2x2=1
4et limx!1
24x2 = 0.
Si x > 1
2, alors 4x2>0et dans ce cas, limx!1
2
x> 1
2
f(x) = +1
Si x < 1
2, alors 4x2<0et dans ce cas, limx!1
2
x< 1
2
f(x) = 1
La droite d’équation y=1
2est asymptote verticale à la courbe de f.
-5 -4 -3 -2 -1 1 2 3 4 5
-5
-4
-3
-2
-1
1
2
3
4
5
x
y
Exemple 14 limite en l’in…ni d’une fonction rationnelle
Déterminer limx!1
2x+6
4x27
Méthode 15 La limite d’une fonction rationnelle (quotient de deux polynômes) en 1 est égale à la limite
en 1 du quotient des monômes de plus haut degré du numérateur et du dénominateur.

1.4 Limites et ordre
Proposition 16 (Compatibilité avec l’ordre) Soit aun réel, +1ou 1. Soit fet gdeux fonctions telles
que lim
x!af(x) = `et lim x!ag(x) = `0.
Si f(x)< g(x)alors ``0.
Théorême 17 (Théorème des gendarmes) Soit trois fonctions f,get htelles que f(x)g(x)h(x)au
voisinage de a(réel ou 1). Si les fonctions fet hont la même limite …nie `au voisinage de a, alors ga
pour limite `au voisinage de a.
Démonstration. On démontre ce théorème dans le cas particulier de +1. Soit Iun intervalle ouvert contenant
`, on doit montrer que Icontient tous les réels g(x)pour xassez grand.
Par hypothèse,
lim
x!+1f(x) = `donc Icontient tous les réels f(x)pour xassez grand, plus précisément, il existe un réel A
tel que si x>Aalors f(x)2I.
lim
x!+1h(x) = `donc Icontient tous les réels h(x)pour xassez grand, plus précisément, il existe un réel
Btel que si x>B alors h(x)2I.
Posons N=max(A;B)alors pour x > N, on a f(x)2Iet h(x)2I. Dire que f(x)g(x)h(x)au
voisinage de +1, signi…e qu’il existe un réel Ctel que pour x>C, on a f(x)g(x)h(x).
Posons M=max(N;C)alors pour x>M, on a f(x)2I,h(x)2Iet f(x)g(x)h(x).
On en déduit que pour x > M, on a g(x)2I; c’est à dire que Icontient les réels g(x)pour xassez grand.
Démonstration.