dc1 4e tech1

L.S.C.J.Gafsa Date : 14 Novembre 2012 Classe :4è.Téch.
Prof :B.Tabbabi Epreuve :Mathématiques Durée :2 heures
DEVOIR DE CONTROLE N°1
Exercice 1 : ( 4 points )
Choisir la réponse exacte (aucune justification n’est demandée ).
1.Un argument du nombre complexe
i3
2e
est :
a)
3
b)
43
c)
3
2.Soit un réel.Les solutions dans de l’équation
2i
iz e z i 0
sont :
a) opposées b) inverses c) conjuguées
3.Soit f une fonction dont la courbe ( C ) dans un repère orthonormé admet la droite
y 2x 1
comme
asymptote au voisinage de ; alors
x
lim f ( x) 2x
est égale à :
a) 1 b) 0 c) 2
4.Soit la fonction g
: x x cos( x)
; alors :
a) g n’a pas de limite en b)
x
lim g(x)
c) g(x) < x pour tout réel x.
Exercice 2 : ( 4 points )
On considère la fonction f définie sur par
2
3
1
1 x sin si x < 0
x
f ( x )
1 x x si x 0
1.a.Vérifier que pour tout x < 0 on a :
22
1 x f ( x ) 1 x   
.
b.Calculer alors
x 0
lim f( x).
2.Etudier la continuité de f en 0.
3.a.Montrer que l’équation f(x) = 0 admet dans
0,1
une solution unique .
b. Vérifier que
21
1.
4.Etudier chacune des limites suivantes :
x
x1
lim f x1
et
+
x1
x1
lim f x1
.
Exercice 3 : ( 6 points )
Soit un réel.On considère dans l’équation
2 i i
( E ):iz (1 ie )z e 0
.
1.a.Vérifier que i est une solution de ( E ).
b. Résoudre alors l’équation ( E ).
2.Dans le plan complexe rapporté à un repère orthonormé direct
O,u,v
,on considère les points A , B et C
d’affixes respectives
ii
A B C
z i,z e et z i e
.
a.Vérifier que A et B appartiennent au cercle de centre O et de rayon 1.
b.Montrer que le quadrilatère OACB est un losange.
3.Dans cette question on prend
3
.
a.Placer dans le repère
O,u,v
les points A , B et C.
b.En déduire un argument du nombre complexe
i3
ie
.
voir verso

Exercice 4 : ( 6 points )
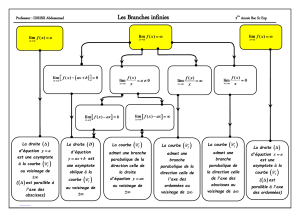
La figure ci-dessous représente la courbe ( C ) d’une fonction f dans un repère orthonormé.
.Les droites y x et y 3 sont des asymptotes à ( C ) au voisinage de et respectivement.
. le point
3
1,2
appartient à la courbe ( C ).
1.Dans cette question,utiliser le graphique pour répondre.
a. Donner
x x x x
f ( x)
lim f( x),lim f( x), lim et lim f ( x) x
x
.
b.Dresser le tableau de variation de f.
c.Déterminer
f ,0 , f 0,2 et f
.
d.Résoudre dans chacune des équations : f(x) 2 et f(x) x.
2.On donne
3
2
3
3
x2
si x 2
x1
f ( x)
3x si x >2
4x
Montrer que par le calcul que la droite
yx
est une asymptote à ( C ) au voisinage de et que la droite
y3
est une asymptote à ( C ) au voisinage de .
Bon travail

- - - - - - - - - - - - - - - - Bon travail