Les nombres complexes prolongent l`ensemble des nombres réels

Terminale STI2D
1
SAES Guillaume
Chapitre 5 : Nombres complexes
Les nombres complexes prolongent l’ensemble des nombres réels. Ils se composent
d’une partie réelle et d’une partie imaginaire. Ils permettent, par exemple, de donner
des solutions à l’équation    .
Leurs applications sont nombreuses en électromagnétisme et en électronique, puisque
leur écriture trigonométrique permet de simplifier la transcription des phénomènes
ondulatoires.
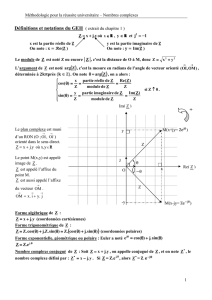
I. Rappels de première
A. Rappel 1 : forme algébrique
Définition : Forme algébrique
L’ensemble  des nombres complexes a les caractéristiques suivantes :
- Il contient le nombre  vérifiant …………………… (solution de …………………………)
- Chaque élément  s’écrit de manière unique  ………………………… où
 est la partie ……………… de  noté ………………… et
 est la partie …………………… de  noté ……………….
- Le conjugué du nombre complexe      est le nombre ………………………………….
Exemple : Soit      et    
    ………………………………………………………………………………………………………………………………
  ………………………………………………………………………………………………………………………………………
 ……………………………………………………………………………………………………………………………………
  ………………………………………………………………………………………………………………………………………

Chapitre 6 : Nombres complexes Terminale STI2D
2
SAES Guillaume
B. Rappel 2 : frome trigonométrique
Définition : Forme trigonométrique
Soit      un nombre complexe non-nul et  le point d’affixe .
- Le module de  est le réel positif ……… tel que …………………………………………………………
( on a la propriété que ………………………)
- L’argument de  est le nombre réel ………… tel que ……………………………………………………
elle vérifie deux choses :
Tout nombre complexe non-nul  peut s’écrire  ………………………………………………………………….
Cette écriture s’appelle la forme trigonométrique de .
Exemple : Soit     
     ……………………………………………………………………………………………………………………………
    ………………………………………………………………………………………………………………………
     ………………………………………………………………………………………………………………………………
Propriété :
-   ……………………………
- …………………………
-  ………………………………………………………
- 
  ………………………………………………………

Chapitre 6 : Nombres complexes Terminale STI2D
3
SAES Guillaume
II. Forme exponentielle
A. Définition
Pour tout nombre réel , on pose …………………………………………………………………………
Définition : Forme exponentielle
Tout nombre complexe  non-nul de module  et d’argument  peut s’écrire sous la
forme   ……………………………………………………….
Cette écriture, avec   , est appelée forme exponentielle du nombre .
Remarque : On a alors   …………………………………………………………………………………………………………….
Exemple : Différentes écritures du nombre complexe     
Forme algébrique
Forme trigonométrique
Forme exponentielle
Exemple : Passage de la forme exponentielle à la forme trigonométrique, puis
algébrique de   
 :
-  
-  
-  

Chapitre 6 : Nombres complexes Terminale STI2D
4
SAES Guillaume
B. Règles de calcul en notation exponentielle
Pour les calculs du type « somme » ou « différence », on utilisera la forme algébrique.
On préférera la forme exponentielle pour les calculs de produits ou de quotients.
Propriété :
Soit  et  des nombres réels et  un nombre entier.
- Produit :    ………………………………………………………
- Puissance :  ………………………………………………………
- Inverse : 
  ………………………………………………………
- Quotient : 
 ………………………………………………………
- Conjugué : 
 ………………………………………………………
Démonstration de la 1ère propriété : Montrons que    ……………… pour   .
On a utilisé une des nombreuses formules d’additivités (voir en annexe).
Exemple : Soit   
 et  
  ………………………………………………………………………………………………………………………………………
   ………………………………………………………………………………………………………………………………………
 …………………………………………………………………………………………………………………………………………