OM . arg z =−arg z [2π] arg z =− π 2 z=∣z∣cosθ+ i∣z∣sinθ z

Les nombres complexes (2)
I Argument d'un nombre complexe
1°)Définitions
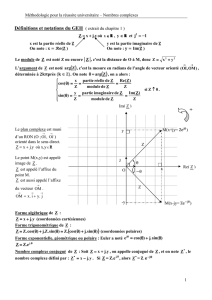
Dans le plan complexe muni du repère orthonormé
O ,  u ; v
on considère le point M d'affixe non nulle
z=a+bi.
Définition
Un argument du nombre complexe non nul z est une
mesure de l'angle orienté
u ; OM 
.
Notation :
Un argument du nombre complexe z est noté arg (z).
Remarque :
Un nombre complexe a une infinité d'arguments, si un des
arguments est θ les autres sont de la forme
θ + k2π, noté également θ [2π].
2°) Propriétés des arguments
Pour tout nombre complexe z non nul :
arg  z=−arg z[2π ]
Pour tout nombre complexe z non nul :
•z est un réel est équivalent à arg (z) = 0 ou arg (z) = π
•z est un imaginaire pur est équivalent à
arg z= π
2
ou
arg z=−π
2
3°) Argument de l'affixe d'un vecteur
Propriété
Soit
AB
le vecteur d'affixe
zB−zA
:
•un argument de l'affixe du vecteur
AB
est égal à
arg zB−zA
.
II Forme trigonométrique d'un nombre complexe
Définition
Dans le plan complexe muni du repère orthonormal
O ,  u ; v
on considère un
point M d'affixe non nulle z.
Si z a pour module
∣z∣
et pour argument arg(z)=θ alors l'affixe de M s'écrit :
z=∣z∣cosθ+i∣z∣sin θ
z=∣z∣(cosθ+isin θ)
z=∣z∣(cosθ+isin θ)
est la forme trigonométrique du nombre complexe z.
Par identification avec la forme algébrique z=a+ib on a
a=∣z∣cosθ
et donc
cos θ=a
∣z∣
, de même on a
sin θ=b
∣z∣
.
Propriété :
Si z = r (cos θ + i sin θ) avec r > 0 alors r (cos θ + i sin θ) est la forme trigonométrique du nombre complexe z et
∣z∣=r
et arg (z) = θ [2π].

Propriété :
Deux nombres complexes
z1=∣z1∣(cos θ1+isin θ1)
et
z2=∣z2∣(cos θ2+isin θ2)
sont égaux si, et seulement si,
∣z1∣=∣z2∣
et
θ1=θ2[2π ]
.
Forme algébrique et forme trigonométrique (passage de l'une à l'autre) :
--------------------------------------------------------------------------------------------------------------------------------------------------
Opération et nombres complexes sous la forme trigonométrique
Propriété : Produit de deux nombres complexes
- Le module du produit
z1z2
est
∣z1z2∣=∣z1∣×∣z2∣
- Un argument du produit
z1z2
est
arg z1z2=arg z1arg z2[2π]
.
Démonstration pour l'argument :
--------------------------------------------------------------------------------------------------------------------------------------------------
Propriété : Puissance d'un nombre complexe
Soit n un nombre entier naturel et z un nombre complexe non nul.
zn
a pour module
∣zn ∣=∣z∣n
et pour argument
arg (zn)=n arg(z)[2π]
.
Propriété : Inverse d'un nombre complexe
Soit z un nombre complexe non nul et
1
z
son inverse :
∣
1
z
∣
=1
∣z∣
et
arg
(
1
z
)
=−arg (z)[2π ]
.
Démonstration pour l'argument:
--------------------------------------------------------------------------------------------------------------------------------------------------
Propriété : Quotient de deux nombres complexes
Soit
z1
et
z2
deux nombres complexes non nuls.
z1
z2
a pour module
∣
z1
z2
∣
=∣z1
∣
∣z2 ∣
et pour argument
arg
(
z1
z2
)
=arg (z1)−arg (z2)[2π ]
.
Démonstration pour l'argument:
--------------------------------------------------------------------------------------------------------------------------------------------------
III Forme exponentielle d'un nombre complexe
Dans le plan complexe muni du repère orthonormal
O ,  u ; v
tout
point M du plan situé sur le cercle de centre O et rayon 1 a pour affixe z
= cos θ + i sin θ (le module est égal à 1).
On appelle f la fonction telle que f(θ) = cos θ + i sin θ.
➢On montre que
fθ× fθ ' = fθθ ' 
, relation
fonctionnelle de la fonction exponentielle.
➢f(0) =1.
On retrouve des propriétés de la fonction exponentielle.
De ces résultats découlent la forme exponentielle d'un nombre complexe
non nul z de module 1 et d'argument θ qui est
z=ei θ=cosθ+isin θ
Cas général :
Définition :
Tout nombre complexe z non nul peut s'écrire sous la forme exponentielle :
z=∣z∣(cos θ+isin θ)=∣z∣ei θ
Propriétés : En appliquant les règles de calcul énoncées sur les nombres complexes et la fonction exponentielle on déduit
que :
r ei θ×r ' ei θ ' =r r ' ei(θ+θ ' )
r ei θ
r ' ei θ ' =r
r ' ei(θ−θ ' )
r ei θ=r e−iθ
r ei θ =r ' ei θ '
équivaut à r = r ' et θ = θ ' [2π].