Quelques interrogations à propos du "tableau de

1
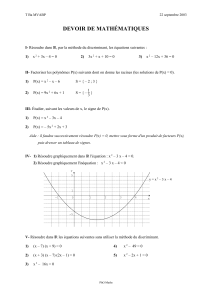
Quelques interrogations à
propos du "tableau de signes"
Dominique Gaud
Régionale de Poitiers
IREM de Poitiers
Membre de la Commission Inter
IREM didactique

2
Cet atelier s’appuie sur la recherche
menée par l’équipe de l’IREM de Poitiers [1]
associée à l’IREM de Paris VII dans le
cadre du projet ADIREM-INRP.
[1] Equipe coordonnée par M.Cheymol, D. Gaud, J.P. Guichard, L. Jussiaume, C.
Robin.

3
Les programmes
Mise en équation ;
résolution algébrique.
Résolution graphique
d’équations et d’inéquations
Résoudre un équation ou une inéquation se
ramenant au premier degré.
Utiliser un tableau de signes pour résoudre
une inéquation ou déterminer le signe d’une
fonction.
Résoudre graphiquement des équation ou
inéquations du type : f(x)=k ; f(x)=g(x) ;
f(x)<g(x) ;…
Pour un même problème, on combinera les apports des
résolutions graphique et algébrique. On précisera les
avantages et les limites de ces différents modes de
résolution.
On pourra utiliser les graphiques des fonctions de
référence et leurs positions relatives.
On ne s’interdira pas de donner un ou deux exemples
de problème conduisant à une équation que l’on ne sait
pas résoudre algébriquement et dont on déterminera
des solutions approchées.
Le libellé diffère sensiblement de celui des programmes antérieurs dans la
mesure où c’est la première fois que l’expression « tableau de signes » est
citée.

4
Actuellement
Utiliser
le tableau de signes
pour résoudre
une inéquation ou
déterminer le
signe d’une
fonction
C’est une
nouveauté

5
Analyse de quelques manuels
En quoi diffèrent et se ressemblent les
différentes présentations des manuels.
Les présentations sont-elles conformes
aux instructions officielles?