Nombres complexes TS z l`ensemble des complexes ℂ contient l

Nombres complexes TS
1. Nombre complexe – Représentation
• Définition un nombre complexe est un nombre de la forme x + i y , où x et y sont deux nombres réels
et i est un nombre imaginaire vérifiant i
2
= – 1 .
• L’ensemble des nombres complexes est noté ℂ .
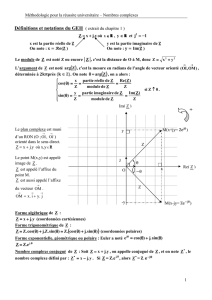
 dans le plan muni d’un repère orthonormal direct ( O ;
u
,
v
) à tout point M correspond un couple ( x ; y ) de réels,
celui de ses coordonnées. Réciproquement, à tout couple de réels correspond un unique point de ce plan.
ainsi, on peut établir une correspondance entre les points du plan et les nombres complexes, souvent notés avec la lettre z .
• Représentation géométrique
le nombre complexe x + i y est l’affixe du point M( x ; y ) ou du vecteur
OM
on écrit : x + i y = z
M
=
OM
z
ou M( x + i y ) on lit : « le point M d’affixe x + i y »
le point M( x ; y ) est l’image de x + i y .
le vecteur
OM
est le vecteur image de x + i y .
le plan muni d’un repère orthonormal direct dans lequel on représente les nombres complexes est appelé plan complexe .
tout point de l’axe des abscisses est l’image d’un nombre réel x + i 0 , avec x réel
noté simplement x . –3 + 0 i = –3 et 0 + 0 i = 0 , ainsi
l’ensemble des complexes ℂ contient l’ensemble des nombres réels R .
tout point de l’axe des ordonnées est l’image d’un nombre complexe 0 + i y ,
avec y réel, noté simplement i y et dit imaginaire pur. 0 + 5 i = 5i , ainsi
l’axe des abscisses (Ox) est l’axe réel et l’axe des ordonnées (Oy) est l’axe imaginaire
• Forme algébrique des nombres complexes
tout nombre complexe z admet une écriture unique de la forme x + i y , où x et y sont deux nombres réels
cette écriture est la forme algébrique de z avec : x , la partie réelle de z , notée Re(z) ;
y , la partie imaginaire de z , notée Im(z) .
la partie imaginaire d’un nombre complexe est un réel ; 3 + i ( 5 + 2i ) n’est pas sous forme algébrique, car 5 + 2i n’est pas un réel.
soit z un nombre complexe, alors :
z est réel si, et seulement si, sa partie imaginaire est nulle ;
z est imaginaire pur si, et seulement si, sa partie réelle est nulle .
deux nombres complexes, z et z’ sont égaux si, et seulement si, ils ont même partie réelle et même partie imaginaire :
z = z’
⇔
(
)
(
)
( ) ( )
Re z Re z'
Im z Im z'
=
=
en particulier, un nombre complexe est nul si, et seulement si, sa partie réelle et sa partie imaginaire sont simultanément nulles.
• Nombres complexes conjugués
Pour tout nombre complexe z de forme algébrique x + i y , le conjugué de z est le nombre complexe x – i y , noté
z
le point M
1
(
z
) est le symétrique de M ( z ) par rapport à l’axe des abscisses (Ox)
un nombre complexe et son conjugué ont même partie réelle et des parties imaginaires
opposées.
Ex : Le conjugué de 2 + 3i est 2 – 3i .

• Module et argument d’un nombre complexe soit z un nombre complexe non nul , d’image M dans le plan muni d’un repère
orthonormal direct ( O ;
u
,
v
) ; M ayant pour coordonnées polaires ( ρ ; θ ) dans ( O ;
u
) .
on dit que : ρ est le module de z , noté
z
. θ est un argument de z , noté arg z .
ainsi le rayon polaire OM vérifie
z
= ρ = OM
l’angle polaire (
u
,
OM
) vérifie arg z = (
u
,
OM
) = θ + 2k
π
où k ∈ Z
on note aussi : arg z = θ [ 2
π
] qui se lit : « θ modulo 2
π
»
si M est un point de coordonnées polaires ( ρ ; θ ) , ses coordonnées cartésiennes sont : x = ρ . cos θ et y = ρ . sin θ
ainsi l’affixe de M , z = x + i y , s’écrit aussi : z = ρ ( cos θ + i sin θ ) forme trigonométrique du nombre complexe z .
on a les relations :
z
= ρ =
2 2
x y
+ ; cos θ =
2 2
x
x y
+
et sin θ =
2 2
y
x y
+
si z = 0 , alors M est en O . La distance OM est nulle . On définit le module de 0 par
0
= 0 .  0 n’a pas d’argument .
 tout point M ( cos θ + i sin θ ) est un point du cercle trigonométrique :
cos i sin
θ θ
+ = 1 et arg ( cos θ + i sin θ ) = θ [2
π
]
2. Calculer avec les nombres complexes
on munit l’ensemble ℂ d’une addition et d’une multiplication qui ont les mêmes propriétés que dans l’ensemble des nombres réels R.
• Addition si z = x + i y et z ’ = x’ + i y’ alors z + z ’ = ( x + x’ ) + i ( y + y’ )
Ex : Si z = 4 + i et z ’ = 2 + 3i , z + z ’ = 6 + 4i
si z et z ’ sont les affixes des points M et M’ ( ou des vecteurs
OM
et
OM '
) ,
z + z ’ est l’affixe du point S ( ou du vecteur
OS
) telle que
OS
=
OM
+
OM '
l’opposé d’un nombre complexe z = x + i y est le nombre noté – z = –x – i y
. les points d’affixes respectives z et – z sont symétriques par rapport à O .
.
-z
=
z
et arg (– z) = arg z +
π
ππ
π
[2
π
]
si A et B sont deux points d’abscisses respectives z
A
et z
B
,
l’affixe
AB
z
du vecteur
AB
est
AB
z
= z
B
– z
A
. soit M le point tel que
OM
=
AB
, alors :
la longueur AB vérifie : OM = AB =
B A
z z
−
l’angle orienté vérifie : (
u
,
OM
) = (
u
,
AB
) = arg (
AB
z
) = arg ( z
B
– z
A
)
Ex : Si z
A
= 4 + i et z
B
= 2 + 3i AB =
B A
z z
− = 2
2
• Addition et nombres complexes conjugués
z + z'
=
z
+
z'
z +
z
= 2 . Re(z)
 si z est non nul de module ρ et d’argument θ : z –
z
= 2i . Im( z )
z
= ρ et arg (
z
) = – θ [2
π
]
Interprétation géométrique
(
u
,
AB
) = arg ( z
B
– z
A
) =
3
4
π
[2
π
]

• Multiplication si z = x + i y et z ’ = x’ + i y’ alors z z ’ = ( x x’ – y y’ ) + i ( x y’ + x’ y )
Ex : ( 1 + i ) ( 1 – i ) = 2 ; ( 5 – 2i ) ( –3 + i ) = –13 + 11 i ; k z = k x + i k y si k ∈ R
tout nombre complexe non nul z = x + i y admet un inverse
1
z
=
2 2
x i y
1
x + i y x
y
−
=+ =
2
z
z
Ex :
1 2 + i
2 i 5
=
−
;
(
)
(
)
1 2i 3 + i
1 2i 1 + 7i
3 i 10 10
+
+= =
−
; le quotient
z' 1
z'
z z
= ×
si z et z’ non nuls , ont pour forme trigonométrique respective z = ρ ( cos θ + i sin θ ) et z’ = ρ’ ( cos θ’ + i sin θ’ ) , alors :
z z ’ = ρρ’ [ cos ( θ + θ’ ) + i sin ( θ + θ’ ) ] on a :
z z'
=
z
.
z'
et arg ( z z’ ) = arg ( z ) + arg ( z ’ ) [2
π
] . 
preuve :
Ex : soit z tel que
z
= 2 et arg ( z ) =
3
π
[ 2
π
] ; z’ tel que
z '
=
2
et arg ( z’ ) =
4
π
−
[ 2
π
]
alors
z z '
= 2
2
et arg ( z z’ ) =
12
π
[ 2
π
] ainsi z z ’ = 2
2
cos i sin
12 12
π π
+
si z et z ’ sont des nombres complexes non nuls , alors :
(1)
1
z
=
1
z
et arg (
1
z
) = – arg ( z ) [2
π
] ;
(2)
z'
z
=
z'
z
et arg (
z'
z
) = arg ( z ’ ) – arg ( z ) [2
π
] ;
(3)
n
z
=
n
z
et arg (
n
z
) = n. arg ( z ) [2
π
] pour n ∈ N ;
. si A , B et C sont trois points distincts du plan, d’affixes z
A
, z
B
et z
C
, alors :
(4)
−
−
C A
B A
z z
z z
=
AC
AB
et arg (
−
−
C A
B A
z z
z z
) = (
AB
,
AC
) [2
π
] ;
preuve :
• Multiplication et nombres complexes conjugués
z ×
××
×
z
=
2
z
;
z z'
=
z
×
××
×
z'
;
n
z
=
(
)
n
z
où n ∈ N .
si
z ≠ 0 :
1
z
=
1
z
et
z'
z
=
z'
z
Ex : Si z = 3 – 2 i , z
z
= 9 + 4 = 13 .
3 + 7 i 3 + 7 i 3 7 i
2 3i 2 3i
2 3i −
  = =
− − − +
  − −
z
= z
on peut aussi écrire
:

• Forme algébrique et formes trigonométriques
z = z’
⇔
(
)
(
)
( ) ( )
Re z Re z'
Im z Im z'
=
=
 z
= z’
⇔
( ) ( )
[ ]
2
z z'
arg z arg z'
π
=
=
z ∈ R
⇔
Im (z) = 0
⇔
z –
z
= 0
⇔
z
= z z ∈ R
⇔
arg ( z ) = 0 ou
π
[2
π
]
⇔
arg ( z ) = 0 [
π
]
z ∈ i R
⇔
Re (z) = 0
⇔
z +
z
= 0
⇔
z
= -z z ∈ i R
⇔
arg ( z ) =
2
π
ou
2
π
−
[2
π
]
⇔
arg ( z ) =
2
π
[
π
]
Forme exponentielle des nombres complexes pour tout nombre réel θ , on pose: cos θ + i sin θ = e
i
θ
tout nombre complexe z non nul , de module ρ et d’argument θ , admet une forme trigonométrique
( appelée forme exponentielle de z ) de la forme z = ρ.e
i
θ
remarque :
Ex :
3 1
i
2 2
+ =
i
6
e
π
;
3
+ i = 2.
i
6
e
π
; –1 –
3
i = 2.
2
i
3
e
π
−
; ; ;
si z et z’ non nuls , ont pour forme exponentielle respective z = ρ e
i
θ
et z’ = ρ’ e
i
θ
’
, alors :
Ex :

• Equations du second degré à coefficients réels
Formules de résolution : a , b et c étant trois réels donnés, avec a non nul, on pose ∆ = b
2
– 4 a c ,
∆ est le discriminant de a z
2
+ b z + c .
Dans ℂ , l’équation a z
2
+ b z + c = 0 admet toujours deux solutions ( confondues si ∆ = 0 ; conjuguées si ∆ < 0 ) .
z
1
=
2
b
a
δ
− −
et z
2
=
2
b
a
δ
− +
où
δ
est un nombre complexe dont le carré est le discriminant
2
δ
= ∆ .
preuve :
Ex :
z
2
– 4 z + 15 = ( z – z
1
) ( z –
1
z
) =
= z
2
– 2 Re( z
1
) z +
2
1
z