Rappel sur les nombres complexes

Université Montpellier II : UFR Sciences Module EEA2 Cours EEA2 : Rappel Complexes
1
Yves Bertrand, [e-mail] Cours2003/2004
Rappel sur les nombres complexes
Les nombres complexes (ou imaginaires) ont été introduits au XVI° siècle (Cardan,
Bombelli) et formalisés au XVIII° (Euler, d'Alembert) pour résoudre les équations faisant
intervenir des racines carrées de nombres négatifs.
¾ Ecriture algébrique
Les nombres complexes sont des nombres de la forme :
z = a + jb, avec a et b réels
j est un nombre tel que : j2=-1
a est la partie réelle de z : a = Re(z)
b est la partie imaginaire de z : b = Im(z)
L'ensemble C des nombres complexes contient tous les nombres réels.
Lorsque b=0, z est réel
Lorsque a=0, z est imaginaire pur
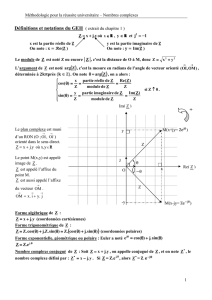
¾ Représentation géométrique et écriture exponentielle
Soit un plan rapporté à un repère orthonormé )v,u,O(
r
r
.
L'axe des abscisses représente l'ensemble des réels.
L'axe des ordonnées représente l'ensemble de imaginaires purs.
M
O
Axe des
imaginaires
purs
a
bz = a+jb
u
r
v
r
Axe des
réels
Plan complexe
ρ
ϕ
Le complexe z = a + jb est appelé affixe du point M(a;b)
Le point M(a;b) est appelé image du complexe z = a + jb.
Le nombre complexe z peut aussi être caractérisé par une écriture qui fait intervenir le
module et l'angle par rapport à l'axe des abscisses du vecteur OM :
ϕρ+ϕρ=ρ= ϕsinjcosez j
ρ est le module de z : ρ = |z|
ϕ est l'argument de z : ϕ = Arg (z)

Université Montpellier II : UFR Sciences Module EEA2 Cours EEA2 : Rappel Complexes
2
Yves Bertrand, [e-mail] Cours2003/2004
¾ Correspondance entre formes algébrique et exponentielle
A partir de la représentation géométrique de z, il vient immédiatement :
a = Re(z) = ρ cos ϕ
b = Im(z) = ρ sin ϕ
22 baz +==ρ
(
)
a
b
Arctg)zarg( ==ϕ
¾ Conjugé d'un nombre complexe
Le conjugé du nombre complexe z = a + jb est le nombre complexe z * = a – jb
En écriture exponentielle, le conjugé de ϕ ρ= j ez , s'écrit : ϕ−
ρ= j e*z
On en déduit les relations suivantes :
(z*)* = z
z.z* = ρ2 = a2 + b2
z + z* = 2 Re(z) = 2a
z - z* = 2j Im(z) = 2jb
Règle pratique : pour trouver la forme algébrique d'un quotient, on multiplie le
numérateur et le dénominateur par l'expression conjugée du dénominateur. Cette opération
rend réel le dénominateur et permet d'écrire le résultat sous la forme algébrique a + jb.
¾ Opérations sur les modules et arguments
A partir de l'écriture exponentielle des nombres complexes, on peut facilement démontrer
les formules suivantes :
• Le module d'un produit est égal au produit des modules :
|z.z'| = |z| . |z'|
• L'argument d'un produit est égal à la somme des arguments :
arg(z.z') = arg(z) + arg(z')
• Le module d'un quotient est égal au quotient des modules :
|z/z'| = |z| / |z'|
• L'argument d'un quotient est égal à la différence des arguments :
arg(z/z') = arg(z) - arg(z')

Université Montpellier II : UFR Sciences Module EEA2 Cours EEA2 : Rappel Complexes
3
Yves Bertrand, [e-mail] Cours2003/2004
D'où les deux règles pratiques :
1 / Pour multiplier deux nombres complexes non nuls,
on multiplie les modules
on ajoute les arguments
2 / Pour diviser deux nombres complexes non nuls,
on divise les modules
on retranche les arguments
Autres relations :
• Argument d'une puissance n : arg(zn) = n arg(z)
• Argument d'un inverse : arg(1/z) = - arg(z)
¾ Formule de Moivre. Formules d'Euler
La formule de Moivre peut se déduire des formules précédentes en écrivant pour un
nombre complexe z de module unité : | zn | = | z |n = 1 :
(cos ϕ + j sin ϕ)n = cos (nϕ) + j sin(nϕ)
A partir des expressions du développement des exponentielles complexes,
ejϕ = cos ϕ + j sin ϕ
e-jϕ = cos ϕ - j sin ϕ
on déduit les relations inverses, dites formules d'Euler :
(
)
ϕ−ϕ +=ϕ jj ee
2
1
cos
(
)
ϕ−ϕ −=ϕ jj ee
j2
1
sin

Université Montpellier II : UFR Sciences Module EEA2 Cours EEA2 : Rappel Complexes
4
Yves Bertrand, [e-mail] Cours2003/2004
Méthode de résolution de circuit
Pour la résolution d'un circuit en courant alternatif par la technique des impédances
complexes, la méthode à suivre est la suivante :
1 / Associer aux variables temporelles leur amplitudes complexes :
• source de tension, prise comme référence des phases : ϕu=0
u(t)=Um cos ωt ↔ m
UU =,
• courants de branche :
i1(t)= I1m cos (ωt+ϕ1i) ↔ 1i
j
m11 eII ϕ
=
i2(t)= I2m cos (ωt+ϕ2i) ↔ 2i
j
m22 eII ϕ
=
. . .
• tensions de nœud :
u1(t)= U1m cos (ωt+ϕ1u) ↔ 1u
j
m11 eUU ϕ
=
u2(t)= U2m cos (ωt+ϕ2u) ↔ 2u
j
m22 eUU ϕ
=
. . .
2 / Exprimer les impédances complexes associées à chaque élément ou ensemble
d'éléments :
• Résistance R ↔ Z
R=R
• Self L ↔ Z
L=jlω
• Condensateur C ↔ Z
C=1/jCω=−j/Cω
• R et L en série ↔ Z
1=R+jLω
• R et C en série ↔ Z
2=R+1/jCω
• R et L en parallèle ↔ Z
3=jRLω/(R+jLω)
• . . .
3 / Utiliser les lois des réseaux continus (superposition, Kirchhoff, Thévenin, …) pour
déterminer les courants de branches Ii et les tensions de nœuds Ui.
4 / Déterminer les valeurs physiques des courants et tensions. En effet, les Ii et Ui ne sont
que des intermédiaires mathématiques. Il faut remonter aux valeurs physiques mesurables :
amplitude et phase des signaux.
Par exemple, après résolution on trouve un courant sous la forme I1 = a1 + jb1. Il faut extraire
son amplitude Im1et sa phase ϕi1.
2
1
2
11m1 baII +==
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=ϕ
1
b
1i a
Arctg 1