Fonction Logarithme népérien 1. De l`exponentielle

Chapitre 7 Terminale S
Fonction Logarithme népérien
Ce que dit le programme :
CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES
Fonction logarithme
népérien x x
On peut introduire la fonction logarithme népérien
Relation fonctionnelle,
a
b
a=b⇔a=eb
x→+∞
x
x=
!"
#
!"
$
($+x)
x
!
%&'()
%&*('
+
,-*.équations fonctionnelles
1. De l'exponentielle au logarithme
1.1) La fonction logarithme népérien
!",.
ℝ
ℝ+∗=
]
/ ;+∞
[
0122"x
t∈ℝ
Autrement dit*"1et 3x ,
1t
t∈ℝ
Théorème et définition *"1
et 3x , 1t
t∈ℝ
4"x 5 11et = x,
1logarithme népérien ln ,lire 6478.
!t 3,x.t 3x.
Exemples :
. *x 39:1et 39:1et 5
t∈ℝ
0,9:.n'existe pas';xx⩽
. *x 3$1
et=$⇔et=e ⇔t=
0
t 3 *$3
.*x 3e , 1
et=e⇔et=e$⇔t=$
0
t 3$*3$
#&< :<4=->!+-?'@-"4ABC@ADDD *$E$

. *x 3F1et3F
t 3F
-1ln 5
!e$3e 3G:$HGHeG3:IHJ
e$KFKeG$Kt KG1CC$KF KG
! Y= e^X $
$ $ $"
t= F≃$L JM
N1
" ln(5)
Conséquences immédiates
$O.4
D=ℝ+∗=
]
/;+∞
[
( ;PQ%R
ℝ
xax
GO.0122$3 e 3$,* .
1.2) Propriétés de réciprocité
Propriétes et definition
$O.*"x
e x=x.
,*$.
GO.*"x
(ex)=x.
,*$".
!exp ln réciproques l'une de l'autre-
*a b
b= a⇔eb=a
,*$.
Démonstration
$O.!"x5 1et 3x, 1
t 3x. STt x"
e x=x.
UB0
GO.&x "!X3ex -X 5 !
"X 5 1et 3X , 1t
t 3X , 1CCt 3,ex.
01
et=X⇔et=ex⇔t=x.
12
B",ex.3x. UB0
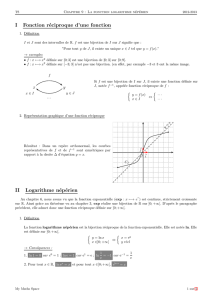
1.3) Sens de variation et limites graphiques
02
(O ;
⃗
i ;
⃗
j),
"Cexp Cln
Ala première
bissectrice1CCV1y = x
M ,x ; y. ∈C %⇔y 3x( %⇔x 3e y ( ⇔M',y ; x. ∈C
W
Propriétes
$O.4strictement croissante ( ;PQ%
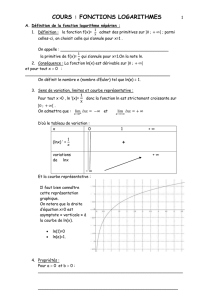
GO.Limites graphiques .4$
x→
x>
x=−∞
".4G
x→+∞
x=+∞
#&< :<4=->!+-?'@-"4ABC@ADDD *GE$

Démonstrations
$O.&""0 < a < b
012a3,ea.b 3,eb.
*A2a Kbe a Ke b !
ℝ,
ln a < ln bUB0
G.Limite en 0+
&-"*x
x KA e x KeA
Kx KeA 12
*x : Kx KeA x KA
0"
10
x→
x>
x=−∞
G".Limite en + ∞
&-"*x
x 5A e x 5eA
x > eA, 12
*x : x > eA, x 5A
0"1
0
x→+∞
x=+∞
Consequences immediates
Propriétes 4( ;PQ%
$O.*"a b1
,*I. a 3b a3b
GO.*"a b1
,*M. a Kb aKb
,*M". ab ab
#&< :<4=->!+-?'@-"4ABC@ADDD *IE$

IO.S"x5 x
,*F. x > x5$
x < KxK$
Exemples
$O.N1eGxP$ 3I,S.
#1"
x∈ℝ
0
DE=ℝ
!a b a 3b a 3b
0""
,Gx P$.3IGx P$3I*
x=−$+ I
G
Conclusion
S=
{
−$+ I
G
}
GO.N1Gx P$I,S1.
#1"
x∈ℝ
0
DE=ℝ
!a b ab ab.
0""
,Gx P$.IGx$I*
x⩽−$+ I
G
Conclusion "
S=
]
−∞ ;−$+ I
G
]
II. Étude de la fonction logarithme népérien
2.1) Fonction dérivée de ln
Propriéte
4"( ;PQ%x 5
'(x)= $
x
Démonstration
&x "@"
x
&x "x
012
x =e(x )
x=e(x)
!"!
X = (x )
X 3,x.
S
eX =x
eX=x
41x x
τ(x ; x)= x – x
x − x
-1"
τ( x ; x)= x – x
x − x
=X − X
eX−e X =$
(
eX− eX
X − X
)
#&< :<4=->!+-?'@-"4ABC@ADDD *ME$

01
x→x
x= x
x→x
X=X
0
x→x
τ(x ; x)= $
X→X
(
eX−e X
X − X
)
S"
ℝ,
"X
0"
1X
-
x→x
τ(x ; x)= $
eX =$
x
0"x
'(x )= $
x
Conclusion4"( ;PQ%x 5
'(x)= $
x
2 ème méthode !"( ;PQ%
68
*"xu,x.3x . !
*x 5 eu( x)3e x 3x S"
u ' (x)×eu(x)=$
u ' (x)×x=$
x≠
u ' (x)= $
x
Conclusion 4"
ℝ+∗
x 5
'(x)= $
x
2.2) Sens de variations de la fonction ln
7Xdirectement
( ;PQ%!x 5
( x)'=$
x>
( ;PQ%
01Y"
x
−∞
+∞
,x.' +
x
+∞
9Q
2.3) Dérivées composées
Propriéte
&u dérivable strictement positive I
ℝ
-
f I x
af ,x.3,u,x.."I
x∈I
f '(x)=u ' (x)
u(x)
1
[ (u)]'=u '
u
.
#&< :<4=->!+-?'@-"4ABC@ADDD *FE$
 6
6
 7
7
 8
8
 9
9
 10
10
1
/
10
100%