Effet Tunnel. Applications.

Le¸con de Physique n◦45 Geoffroy Aubry - Moussa Dicko
Effet Tunnel. Applications.
Correction : Lo¨ıc AUVRAY
Pr´erequis
Postulats de la M´ecanique Quantique, en particulier l’´equation de
Schr¨odinger. Cette le¸con est une application directe de cette derni`ere.
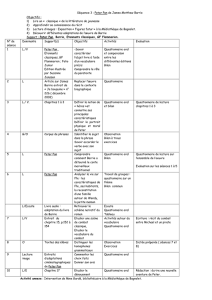
Plan
1 Introduction 1
2 Travers´ee d’une barri`ere de potentiel 1
2.1 G´en´eralis´es : barri`ere quelconque . . . . . . . . . . . . . . . . . . 1
2.2 Transparence d’une barri`ere rectangulaire . . . . . . . . . . . . . 3
3 Applications 4
3.1 Travers´ee Classique .......................... 4
3.2 Microscope `a effet tunnel . . . . . . . . . . . . . . . . . . . . . . 5
3.3 Radioactivit´e α............................ 5
3.3.1 Position du probl`eme . . . . . . . . . . . . . . . . . . . . . 5
3.3.2 Mod`ele de Gamow . . . . . . . . . . . . . . . . . . . . . . 6
4 Conclusion 7
5 Questions, commentaires et remarques 7
6 Bibliographie 7
1 Introduction
L’effet Tunnel fut pr´edit d`es le d´ebut de la m´ecanique quantique, et mis en
´evidence d`es le fin des ann´ees 30 pour expliquer diff´erents ph´enom`enes (Fow-
ler/Nordheim 1928 pour l’extraction d’´electrons d’un m´etal sous l’effet d’un
champ ´electrique fort, Gamow 1928 pour la radioactivit´e α, Frenkel 1930 sur la
resistance de contact entre deux mat´eriaux conducteurs).
2 Travers´ee d’une barri`ere de potentiel
2.1 G´en´eralis´es : barri`ere quelconque
Traitons le probl`eme `a une dimension suivant. Une onde plane de particules
arrive de la gauche vers la droite et se heurte `a la barri`ere de potentielle. Ces
1

Fig. 1 – Situation physique
particules ont une ´energie purement cin´etique E=p2
2m< Vmax. Classiquement,
la particule ne peut pas passer dans la zone III et doit repartir dans l’autre sens.
D´ecrivons le probl`eme `a l’aide du formalisme quantique. ´ Ecrivons l’´equation
de Schr¨odinger pour nos particules :
−i~∂Ψ
∂t (x,t) = b
HΨ(x,t) (1)
avec ici b H=
bp2
2m+V(x)
Pour un syst`eme isol´e ind´ependant du temps, on peut ´ecrire Ψ(x,t) = e
−itE
~ϕ(x),
et l’´equation devient :
b
Hϕ(x) = Eϕ(x) (2)
Soit en utilisant le fait que bp2↔ −i~∂
∂x ,
∂2ϕ
∂x2(x) + 2m ~2(E−V(x))ϕ(x) = 0 (3)
R´egions I et III : V= 0 donc E−V > 0 L’´equation peut donc s’´ecrire :
∂2ϕ
∂x2(x) + κ2ϕ(x) = 0 (4)
avec κ=√2mE
~
Les solutions g´en´erales de l’´equation s’´ecrivent :
ϕI(x) = Aeiκx +Be−iκx (5a)
ϕIII (x) = A0eiκx +B0e−iκx (5b)
La situation physique ´etudi´ee nous impose qu’il n’y ait pas de particules
venant de la droite dans la r´egion III. Donc B0= 0.
Remarque : ϕI(x) et ϕIII ne sont pas normalisables car
repr´esentent des ondes planes qui sont non physiques car as-
soci´ees `a une ´energie infinie.
2

ΨI(x,t) = Aeiκx +Be−iκxe
−itE
~(6a)
ΨIII(x,t) = A0eiκxe
−itE
~(6b)
Le nombre de particules qui passe par unit´e de temps au point d’abscisse
xest donn´e par le courant de probabilit´e j=p
m|Ψ|2, donc est proportionnel `a
|Ψ|2.
Une particule arrivant de la source a 2 devenirs possibles :
– soit elle est r´eflechie sur la barri`ere et repart vers −∞. On d´efinit alors un
coefficient de reflexion :
R=nombre de particules r´efl´echies par unit´e de temps
nombre de particules incidentes par unit´e de temps =
B
A
2
(7)
– soit elle est passe `a travers la barri`ere. On d´efinit alors un coefficient de
transmition :
T=nombre de particules transmises par unit´e de temps
nombre de particules incidentes par unit´e de temps =
A0
A
2
(8)
Avec R+T= 1. Dans pas mal de situations physiques, T << 1, mais nous
nous int´eresserons ici justement aux cas o`u T6= 0 et o`u une particule peut
passer une barri`ere de potentiel mˆeme avec une ´energie cin´etique inf´erieure au
pic de potentiel (situation impossible classiquement).
2.2 Transparence d’une barri`ere rectangulaire
Int´eressons nous maintenant `a un cas que l’on peut r´esoudre analytiquement.
Les calculs ont d´ej`a ´et´e ´et´e effectu´es dans les r´egions I et III.
R´egions II : V−E > 0
∂2ϕ
∂x2(x)−α2ϕ(x) = 0 (9)
avec α=√2m(V−E)
~Les solutions g´en´erales de l’´equation s’´ecrivent :
ϕIII (x) = A00eαx +B00eαx (10)
Raccordement L’´equation de Schr¨odinger nous impose que la solution soit
continue. On peut le voir de deux mani`eres diff´erentes. Soit analytiquement, et
pour ceci voir l’explication du Dalibard, soit comme ceci : la fonction d’onde et
sa d´eriv´ee repr´esentent (ou plutˆot leur module au carr´e) une quantit´e physique
(respectivement le nombre de particules par unit´e de volume et le nombre de
particules qui passent `a l’endroit consid´er´e). Vu que notre potentiel n’est pas
trop bizarre (il a seulement des discontinuit´es finies), ceci nous impose que ϕet
ϕ0soient continus en tout points de l’espace, et en particulier en 0 et en a, ce
qui nous donne les diff´erentes relations :
3

– Continuit´e de ϕ:
x= 0 A+B=A00 +B00 (11a)
x=a A0eiκa =A00eαa +B00e−αa (11b)
– Continuit´e de ϕ0:
x= 0 iκ(A−B) = α(A00 −B00) (12a)
x=a iκA0eiκa =α(A00eαa −B00e−αa) (12b)
Soit un syst`eme avec 5 inconnues et 4 ´equations. Mais comme nous cherchons
le rapport de deux des inconues, nous pouvons ´ecrire l’une en fonction de l’autre.
On cherche donc `a r´esoudre de syst`eme :
1 1 −1−1
0 0 eαa e−αa
iκ −iκ −α α
0 0 αeαa −αe−αa
A
B
A00
B00
=
0
A0eiκa
0
iκA0eiκa
qui nous donne apr`es r´esolution :
A
A0
2
= 1 + 1
4sh2(αa)α κ+κ α2(13)
Soit finalement :
1
T= 1 + V2
0
4E(V0−E)sh2 p2m(V0−E) ~a!(14)
Remarque : G´en´eralement, dans la plupart des cas qui nous
int´eressent lorsqu’on ´etudie l’effet tunnel, l’argument dans le
sh est suffisament supp´erieur `a 1 pour qu’on puisse dire sh ∼
exp/2. C’est l’approximation qui est faite dans beaucoup d’ou-
vrages.
3 Applications
3.1 Travers´ee Classique
Donn´ees :
–m= 50 g
–E=mgz0, avec z0= 5 cm
–V0=mgh, avec h= 10 cm
–a= 1cm
Application num´erique : 1
T= 1 + sh2(4,7.1030), soit T∼10−4.1030 . Si on
cherchait `a ´ecrire tous les 0 de ce nombre avec des chiffres de 2 mm, il faudrait
8.1027 m, soit 800 milliards d’ann´ees lumi`eres (la taille de l’univers connu est
de 15 milliards d’ann´ees lumi`eres).
4

3.2 Microscope `a effet tunnel
En approchant une pointe conductrice taill´e tr`es finement (quelques atomes
seulement) `a proximit´e (d∼5˚ A) d’une surface conductrice, et en imposant une
diff´erence de potentiel de quelques mV , on mesure un courant de quelques nA.
Le nombre d’´electrons qui passent `a travers la barri`ere de potentiel (ici : c’est
le vide entre les deux ´electrodes conductrices) diminue de mani`ere exponentielle
avec la largeur de la barri`ere. En analysant le signal d’erreur d’un asservissement
sur le courant passant dans le circuit, on peut avoir acc´es `a une cartographie
tr`es pr´ecise de la surface mesur´ee (r´esolution de l’ordre de 0,1˚ Aen vertical, et
de l’ordre de 5 ˚ Aen horizontal1.
3.3 Radioactivit´e α
3.3.1 Position du probl`eme
Pour des noyaux ayant un nombre de nucl´eons devenant trop important,
la r´epulsion coulombienne entre protons prend des valeurs significatives par
rapport `a l’interaction forte qui assure la coh´esion du noyau. On assiste au
ph´enom`ene de saturation, qui donne lieu `a la d´esint´egration αqui est un cas
particulier d’une fission spontann´ee.
Par exemple :
226
88 Ra →224 86 Rn +4 2α
La particule αest ´emise avec une ´energie de 4,78 MeV .
Si on sch´ematise le potentiel auquel est soumis la particule en fonction de sa
distance au noyau, on voit une barri`ere de potentiel tr`es grande devant l’´energie
avec laquelle la particule sort du noyau. Gamow a propos´e une explication `a ce
ph´enom`ene en 1928. Il suppose que la particule αpr´e-existe dans le noyau et
cogne sur les parois. Elle a une probabilit´e non nulle de franchir la barri`ere de
potentiel par effet tunnel.
Fig. 2 – Radioactivit´e alpha
1La limite de r´esolution horizontale est due `a la taille de la pointe qui sonde la surface.
On choisit une pointe tr`es dure pour ´eviter que les atomes d´eplacent tout seuls `a la surface
de celle ci afin de former une pointe sph´erique (ph´enom`ene de tension superficielle `a l’´echelle
microscopique).
5