Chapitre 20 DÉRIVATION Enoncé des exercices

Chapitre 20
DÉRIVATION
Enoncé des exercices
1Les basiques
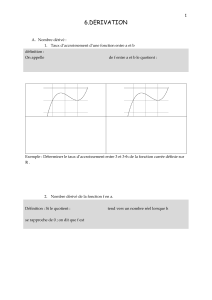
Exercice 20.1 Simplifier la dérivée de f(x) = sin xtan x+ 2 cos x−2
Exercice 20.2 Soit f(x) = 1−ch x
xsi x= 0, peut-on prolonger fen une fonction continue sur R. Le prolongement
obtenu est-il dérivable sur R?
Exercice 20.3 Soit f(x) = x
x
, peut on prolonger fsur R
+
,le prolongement est-il dérivable sur R
+
?
Exercice 20.4 Etudier la dérivabilité de f(x) = sin xsin 1
xsi x= 0 et f(0) = 0
Exercice 20.5 Déterminer apour que la fonction fdéfinie par f(x) = √xsi 0≤x≤1et f(x) = ax
2
+ 1 si x > 1
soit dérivable sur R
∗
+
.
Même question avec f(x) = ax
2
+bx + 1 si x > 1.
Exercice 20.6 Simplifier f(x) = 2 arctan 
1−x
x
+ arcsin (2x−1) (Déterminer D
f
, D
f
′
et calculer f
′
(x))
Exercice 20.7 Calculer la dérivée énième de la fonction fdéfinie par f(x) = x
2
+x+ 1e
−x
Exercice 20.8 On considère la suite (u
n
)
n
définie par u
0
∈0,
4
3
et ∀n∈N, u
n+1
=
1
3
4−u
2
n
Justifier rapidement que ∀n∈N, u
n
∈0,
4
3
A l’aide de l’inégalité des accroissements finis, montrer que (u
n
)
n
converge vers 1.
Exercice 20.9 Calculer la dérivée énième de 1
n!x
n
(1 + x
n
).
Exercice 20.10 Soit fdéfinie sur Rpar
∀x∈R,f(x) = ln 1 + x
2
ln (x)
(x−1)
Peut-on prolonger fen une fonction continue sur l’intervalle [0,+∞[? Le prolongement obtenu est-il dérivable en
x= 0 ?
Exercice 20.11 Soit P∈R[X],on définit fpar f(x) = P1
1−xe
1
1−x
, montrer que f
′
(x) = Q1
1−xe
1
1−x
où Q∈R[X]. Quelle relation existe-t-il entre Pet Q? (voir aussi l’exercice 20.28)

2. LES TECHNIQUES CHAPITRE 20. DÉRIVATION
Exercice 20.12 Soient fet gdéfinies par f(x) = cos xet g(x) = xsin x, montrer que lorsque les courbes représen-
tatives de fet de gse coupents les tangentes au point d’intersection sont perpendiculaires.
Exercice 20.13 Soit h:R−→ Rdéfinie par ∀x∈R,h(x) = (x−E(x)), etudier la dérivabilité de gdéfinie sur R
par g(x) = h(x) (h(x)−1).
2Les techniques
Exercice 20.14 Soit f(x) = x
2
sin 1
x. Peut-on prolonger fen une fonction continue sur R?
Le prolongement est-il dérivable sur R? Si oui, donner l’expression de la dérivée et préciser s’il est de classe C
1
sur R
(i.e. la dérivée est-elle continue sur R?)
Exercice 20.15 La fonction fdéfinie par f(x) = cos (√x)est-elle dérivable en x= 0 ? Si oui, est-elle de classe C
1
?
Exercice 20.16 Soit fdéfinie par f(x) = arctan 1 + 1
x
2
et f(0) = π
2,fest-elle C
1
sur R?
Exercice 20.17 Calculer la dérivée énième de f(x) = x
n
(1 + x)
n
.
En considérant le coefficient de x
n
,en déduire une expression simple de
n
k=0
C
k
n
2
et montrer que
n
k=0
2
k
C
k
n
2
=
n
k=0
C
k
n
C
k
n+k
Exercice 20.18 Soit fcontinue et dérivable sur R
+
telle que f(0) = f
′
(0) = 0.
1. On définit ϕpar ϕ(0) = 0 et ϕ(x) = f(x)
xsi x= 0.Etudier la continuité de ϕsur R
+
.
2. On suppose qu’il existe a > 0tel que f(a) = 0. Montrer qu’il existe c > 0tel que la tangente au point d’abscisse
cpasse par l’origine du repère.
3. Question (∗): Montrer le même résultat si on remplace l’hypothèse ∃a > 0, f (a) = 0 par f(1) = 1
f
′
(1) = 0
Exercice 20.19 On considère la fonction f(x) = 1
1 + x
2
, cette fonction est clairement de classe C
∞
sur R.
1. Montrer par récurrence qu’il existe un polynôme P
n
(X)tel que,
∀x∈R, f
(n)
(x) = P
n
(x)
(1 + x
2
)
n+1
et que
P
n+1
(x) = 1 + x
2
P
′
n
(x)−2 (n+ 1) x P
n
(x)
2. En dérivant f, on constate que ∀x∈R,1 + x
2
f
′
(x) + 2xf(x) = 0. En utilisant la formule de Leibniz sur cette
égalité que l’on dérivera nfois, établir que
P
n+1
(x) + 2 (n+ 1) x P
n
(x) + n(n+ 1) 1 + x
2
P
n−1
(x) = 0
En déduire que
P
′
n
(x) = −n(n+ 1) P
n−1
(x)
Exercice 20.20 Soit α∈]0,1[, pour tout entier n > 0,on pose u
n
=
n
k=1
1
k
α
—2/19— G´  H - E M -() 2009

CHAPITRE 20. DÉRIVATION 2. LES TECHNIQUES
1. A l’aide de l’inégalité des accroissements finis, prouver que
∀k∈N
∗
,1−α
(k+ 1)
α
≤(k+ 1)
1−α
−k
1−α
≤1−α
k
α
2. En déduire un encadrement de 1
k
α
pour k≥2
3. En déduire un encadrement de u
n
puis un équivalent.
4. Application : donner un équivalent de 1 +
1
√2
+
1
√3
+... +
1
√n
quand ntend vers +∞.
Exercice 20.21 Calcul de 
n
k=0
kn
ka
k
b
n−k
1. Soit α∈R, calculer la dérivée k-ième de f
α
(x) = xe
αx
.
2. Soient (a, b)∈R
2
,en écrivant que f
a+b
(x) = f
a
(x)e
bx
exprimer f
(n)
a+b
(x)en fonction des dérivée k-ième de f
a
.
3. En déduire la valeur de
n
k=0
kn
ka
k
b
n−k
Exercice 20.22 Soit f: [a, b]→Rune fonction continue et strictement positive, dérivable sur ]a, b[.Montrer qu’il
existe c∈]a, b[tel que
f(b)
f(a)=e
(b−a)
f′(c)
f(c)
Peut-on remplacer l’hypothèse positive sur [a, b]par non nulle sur [a, b]?
Exercice 20.23 Trouver toutes les fonctions dérivables en 0et telles que
∀(x, y)∈R
2
,f(x+y) = f(x) + f(y) + 2xy
Exercice 20.24 Soit f(x) = (x−1)
1
x−1
, peut on prolonger fen une fonction continue sur R? Le prolongement
obtenu est-il dérivable en x= 1 ?
Question ++ : La dérivée obtenue est-elle continue en x= 1 ?
Exercice 20.25 Soit fde classe C
1
sur [a, b]à valeurs dans Rtelle que f
′
(b) (f(b)−f(a)) <0. Montrer que f
′
s’annule sur ]a, b[.
Exercice 20.26 Soit fdérivable sur [a, +∞[telle que f
′
(x)−−−−−→
x→+∞
0,montrer que f(x)
x−−−−−→
x→+∞
0.
Exercice 20.27 On suppose connu l’existence (et l’unicité) d’un polynôme T
n
tel que ∀θ∈R,T
n
(cos θ) = cos (nθ).
Montrer que T
n
est solution de l’équation différentielle
x
2
−1y
′′
+xy
′
=n
2
y
Exercice 20.28 Soit fla fonction définie sur Ipar f(x) = 1
1−xe
1
1−x
.
1. Prouver par récurrence que, pour tout entier naturel n, il existe un polynôme P
n
tel que :
f
(n)
(x) = P
n
1
1−xe
1
1−x
pour tout réel xappartenant à I.
La démonstration permet d’exprimer P
n+1
(X)en fonction de P
n
(X), P
′
n
(X)et X. Expliciter cette relation.
2. Préciser P
0
, P
1
, P
2
et P
3
.
3. En dérivant nfois les deux membres de l’équation (E),prouver que pour tout entier positif n:
P
n+1
(X) = (2n+ 1) X+X
2
P
n
(X)−n
2
X
2
P
n−1
(X)
—3/19—
G´  H - E M -() 2009

3. LES EXOTIQUES CHAPITRE 20. DÉRIVATION
Exercice 20.29 Soit P∈R[X]scindé à racines simples. Montrer que Pne peut avoir deux coefficients consécutifs
nuls (de degré inférieur au degré de P).
Exercice 20.30
1. Soit ϕdéfinie au voisinage de 0telle que ϕ(x)−−−→
x→0
0,montrer
∀ε > 0,∃N∈N,n≥N=⇒
n
k=0
k
n
2
ϕk
n
2
≤ε
Que peut-on en déduire ?
2. Soit f: [0,1] −→ Rdérivable en 0, étudier la suite (u
n
)définie par
u
n
=
n
k=0
fk
n
2
3Les exotiques
Exercice 20.31 Soient (a, b)∈R
2
et n≥2.Montrer que le polynôme X
n
+aX +badmet au plus trois racines réelles
distinctes.
Exercice 20.32 Soit f(x) = tan x, à l’aide la relation f
′
= 1 + f
2
et de la formule de Leibniz, déterminer un
algorithme de calcul de a
n
=f
(n)
(0)
n!.
Exercice 20.33 Soient a < b et f: [a, b]→Rune fonction continue sur [a, b],dérivable sur ]a, b[.Montrer qu’il
existe c∈]a, b[tel que 1
a−c< f
′
(c)<1
b−c
On utilisera la fonction F(x) = (x−a) (x−b) exp (f(x)).
4Les olympiques
Exercice 20.34 Soit f: [a, b]→R, de classe C
2
sur [a, b]et 3fois dérivables sur ]a, b[. Montrer qu’il existe c∈]a, b[
tel que
f(b) = f(a) + b−a
2(f
′
(a) + f
′
(b)) −(b−a)
3
12 f
(3)
(c)
En déduire que ∀x∈0,
1
√3
,0≤arctan (x)−
x
2
2+x
2
1+x
2
≤
x
3
6
Indication : utiliser φ(t) = f(t)−f(a)−
t−a
2
(f
′
(a) + f
′
(t)) +
(t−a)
3
12
Koù Kest à choisir.
Exercice 20.35 Résoudre l’équation
5
x
+ 2
x
= 4
x
+ 3
x
où x∈R
∗
+
Exercice 20.36 Soit f∈ C
2
(R)telle que ∀(x, y)∈R
2
,f(x+y)f(x−y)≤f(x)
2
.Montrer que ∀x∈R,f(x)f
′′
(x)≤
f
′
(x)
2
—4/19— G´  H - E M -() 2009

Chapitre 20
DÉRIVATION
Solution des exercices
1Les basiques
Exercice 20.1 Très simple, la fonction est définie et dérivable sur Rprivé des k
π
2
où k∈Zet
f
′
(x) = cos xtan x+sin x
cos
2
x−2 sin x=sin x cos
2
x−sin x= sin x1 cos
2
x−1
=sin
3
x
cos
2
x
Exercice 20.2 La fonction fest continue et dérivable sur R
∗
d’après les théorèmes généraux. Le seul problème est en
x= 0. On a f(x)∼
x→0
−x
2
2
x=−x 2−−−→
x→0
0, ainsi f(x)−−−→
x→0
0. On pose f(0) = 0,le prolongement est alors continue
en x= 0. On regarde alors le taux d’accroissement f(x)−f(0)
x−0=1−ch x x∼
x→0
−1
2. Le prolongement obtenu est
donc dérivable en 0et ainsi sur R.
Exercice 20.3 On a f(x) = e
xln x
,on sait (croissance comparées) que xln x−−−→
x→0
0, ainsi par continuité de l’expo-
nentielle en x= 0,on a e
xln x
−−−→
x→0
e
0
= 1. On pose donc f(0) = 1 pour obtenir une fonction continue sur R
+
(la
continuité sur R
∗
+
découle des théorèmes généraux).On considère ensuite f(x)−f(0)
x−0=e
xln x
−1
x.De e
u
−1∼
u→0
u
et de u=xln x−−−→
x→0
,on déduit que e
xln x
−1
x∼
x→0
xln x
x= ln x−−−→
x→0
−∞. Le prolongement n’est pas dérivable en 0,
il admet cependant une tangente verticale.
Exercice 20.4 On a sin x−−−→
x→0
0et sin 1
xest bornée donc f(x)−−−→
x→0
0. La fonction fest donc continue (ce qui est
une condition nécessaire). Puis f(x)−f(0)
x−0=sin x xsin 1 x. Puisque sin x xa une limite finie et non nulle, si fest
dérivable en 0,on en déduit que sin 1
x=1
sin x
x
×f(x)−f(0)
x−0a aussi une limite, ce qui est absurde. La fonction
n’est donc pas dérivable.
Exercice 20.5 Il est clair que fest continue sur ]0,1[ ∪]1,+∞[. Examinons la dérivabilité en x= 1. Une condition
nécessaire est que fsoit continue en 1. On a f(1) = √1par définition et lim
x→1
−
f(x) = lim
x→1
−
√x=√1 = 1 et
lim
x→1
+
f(x) = lim
x→1
+
ax
2
+ 1 = a+ 1. Pour que fsoit continue en x= 1,il faut et il suffit que a= 0.
Dans ce cas f(x) = 1 si x > 1et ainsi fest dérivable à droite en 1avec f
′
d
(1) = 0. Mais sur [0,1] ,on a f(x) = √x