Fonctions dérivées

Fonctions dérivées
I- Nombre dérivé d’une fonction en x
1- Définition
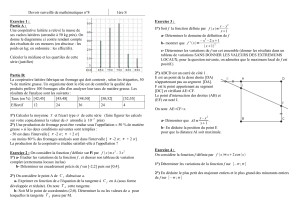
C est la courbe d’une fonction f
Mo est un point fixe de la courbe C d’abscisse xo
M est un point variable de C d’abscisse xo + h
Le coefficient directeur de la sécante (Mo M) est
00
( ) ( )
() f x h f x ah h
(Aussi appelé taux d’accroissement de f en xo)
Quand h tend vers 0, la sécante tend vers une position limite T. Dans cette
position limite, (MoM) est appelée tangente.
Def : le coefficient directeur de la tangente T, quand il existe, est appelé
nombre dérivé de f en xo et on le note
0
'( )fx
Ainsi :
00
00
( ) ( )
'( ) lim
h
f x h f x
fx h
Si
0
'( )fx
existe on dit que f est dérivable en xo
Il n’existe pas , en particulier, quand : la tangente est verticale ou quand Mo est
un pic (un point anguleux) de la courbe.

2- Exemple d’équation de tangente
Avec la fonction f définie par
2
()f x x
Equation de la tangente T au point Mo d’abscisse xo = 2 :
Son coefficient directeur est
'(2) 2 2 4f  
L’ équation de T est donc du type
4y x b
, où b est un réel que l’on détermine
en écrivant que Mo est un point de la tangente.
0(2;4) 4 4 2
4
4 4
M T b
b
T y x
3- Approximation affine locale
Pour h voisin de 0 ,
0 0 0
( ) ( ) . '( )f x h f x h f x  
(en effet , au voisinage de xo, la courbe et la tangente sont quasi confondues)
Ainsi avec
2
()f x x
et
01x
On a :
0
( ) 1
'( ) 2
'(1) 2
fx
f x x
f
On obtient
2
(1 ) 1 2hh  
12h
est une approximation affine de
2
(1 )h
pour h voisin de zéro.
Application :
2
2
(1.01) 1 2 0.1
(1.01) 1.02

II- Dérivée des fonctions usuelles
Fonction dérivée
Définition : Soit f une fonction dérivable sur un intervalle I de R. Alors la
fonction qui à tout x de I associe
'( )fx
est appelée fonction dérivée de f sur I
est noté
'f
Théorème : une fonction polynôme ou rationnelle est dérivable sur son ensemble
de définition ; la fonction
xx
est dérivable sur R*+
f
'f
Ensemble de dérivabilité
a
(constante)
0
R
x
1
R
.a x b
a
R
2
x
2x
R
3
x
2
3x
R
n
x
nZ
*
1
.n nx 
R ou R* suivant le signe
de n
x
1
2x
R*+
1
x
2
1
x
R*
sin x
cosx
R
cosx
sinx
R
tanx
2
1
cos x
R-
{}
2k
kZ

III- Opérations sur les dérivées
Dans ce tableau u et v sont des fonctions dérivables sur un intervalle I
()fx
'( )fx
uv
''uv
.uv
' . 'u v uv
.ku
.'ku
1
u
avec u(x)
0 sur I
2
'u
u
u
v
avec v(x)
0 sur I
2
'. . 'u v uv
v
n
u
nZ
*
1
.'
n
nu u
u
'
2uu
sin.u
'cos.uu
cos.u
'sin.uu
tan.u
2
'
cos
uu
Résumé concocté par Camille Kerbaul , élève de 1° S et validé par Guy Marion