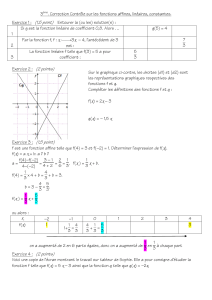
CHAPITRE 3

1
CHAPITRE 3
LES FONCTIONS.
I - Notion de fonction.
Ce chapitre est une initiation à la notion de fonction.
Il sera approfondi en seconde.
a) Image et antécédent.
Soit x un nombre relatif. Une fonction, f, transforme cette valeur x en une
autre valeur y.
Le résultat y peut être obtenu par calcul ou lecture (dans un tableau ou sur un
graphe).
Deux écritures sont possibles pour dire que l’on applique la fonction f à x et que
l’on obtient y. Je dois les connaître toutes les deux!
f : x y ou f(x) = y
Exemples :
a) f : x 2x+1
f(x) = 2x+1
Si le texte me donne x = 2 alors :
f : x 2x+1 devient 2 2 2 + 1
2 5
OU
f(2) =2 2 + 1
f(2) =5
On dit que l’image de 2 est 5 ;
L’antécédent de 5 est 2.
b) f : x 9x²+3x-2
f(x) = 9x²+3x-2
y est obtenu par le calcul de 2x+1
y est obtenu par le calcul de 9x²+3x-1
Je pense à respecter
les priorités
opératoires.
Le nombre 2 est
transformé en 5.
Y = 5

2
Si le texte me donne x = -3 alors
f : x 9x²+3x-2 devient -3 9 (-3)² + 3 (-3) – 2
-3 9 9 – 9 – 2
-3 81 –9 + 2
-3 74
OU
f(-3) = 9 (-3)² + 3 (-3) – 2
f(-3) = 9 9 – 9 – 2
f(-3) = 81 –9 + 2
f(-3) = 74
l’image de -3 est 74 ;
-3 a pour image 74 .
L’antécédent de 74 est –3.
-3 est l’antécédent de 74.
Autres exemples.
c) Soit la fonction f : x x² + 6
Quelle l’image de 5 ?
d) Soit la fonction f(x) = 3x-4.
Quelle l’image de –2 ?
Quel l’antécédent de –4 ? (Je vais retrouver une équation)
b) Tableau de valeurs.
Dans les activités de découvertes j’ai appris que les valeurs d’une fonction
peuvent être données dans un tableau.
Je reprends les exemples a) et b).
a) f : x 2x+1
Un tableau de valeurs possible serait:
x
-3
2
5
-1
0
3,4
1,75
-0,8
f(x)
-5
5
11
-1
1
7,8
4,5
-0,6
Je pense à respecter
les priorités
opératoires et à
appliquer les règles
des signes.
Le nombre -3 est
transformé en 74.
Y = 74

3
Les valeurs de x sont soit données par le texte, soit choisi par moi-même.
b) f(x) = 9x²+3x-2
Pour cette fonction, j’ai utilisé le logiciel Excel.
J’ai appris en quatrième à rentrer une formule pour faire un calcul. J’applique
cette connaissance pour compléter un tableau de valeurs d’une fonction.
Autres exemples :
Je reprends les fonctions c) et d).
c) Remplir le tableau suivant :
x
-3
-2
0
5
f(x)
d) Remplir le tableau d’Excel suivant en écrivant la formule saisie en B2 et
non le résultat.
x
-5
-4,6
-3
-2,25
0
1,05
4,22
9,45
f(x)
208
174,64
70
36,8125
-2
11,0725
170,9356
830,0725
J’ai rentré la
formule de calcul
avec l’adresse de la
cellule donnant la
valeur de x.
J’ai étiré la formule jusqu’en I2. Comme j’ai saisi B1, au
lieu de –5, lorsque j’étire ma formule le logiciel change
automatiquement les valeurs de x.

4
c) Représentation graphique.
D’après les activités de découverte, je sais aussi que les fonctions se
représentent graphiquement.
Grâce à ces représentations je peux lire une image ou un antécédent.
Je reprends les fonctions a) et b) des exemples.
a) f : x 2x+1
Cette fonction peut se représenter graphiquement comme suit :
Fonction exemple a)
-15
-14
-13
-12
-11
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
-8 -6 -4 -2 0 2 4 6 8
valeur de x
valeur de f(x), y.
f(x)
Sur ce graphe, je peux lire les images de 2, 0, 6.
Je peux également lire les antécédents de –5, 5 , -1.
b) f(x) = 9x²+3x-2
Je peux également lire des images et des antécédents à l’aide de ce graphe.

5
II- Fonctions linéaires (rappel du chapitre 6)
Dans le chapitre de la proportionnalité j’ai appris à représenter graphiquement
une situation de proportionnalité.
Je sais maintenant que cette notion est liée au fonction linéaire.
Une fonction linéaire de coefficient a est définie par la relation suivante :
à x un nombre relatif quelconque on fait correspondre le nombre ax.
f : x ax OU f(x) = ax
Sa représentation graphique est une droite passant par l’origine du repère.
Le nombre a est appelé coefficient directeur de la droite.
J’ai appris :
- à déterminer par le calcul l’image d’un nombre donné ;
- à déterminer par le calcul l’antécédent d’un nombre donné ;
- à retrouver l’expression d’une fonction linéaire connaissant un nombre
et son image ;
- à représenter graphiquement une fonction linéaire ;
- à exploiter la représentation graphique d’une fonction linéaire.
III- Fonctions affines.
a) Définition.
Soient a et b deux nombres relatifs connus et fixés.
La fonction affine de coefficients a et b est définie par la relation suivante :
à un nombre relatif x on associe le nombre ax + b.
Exemples :
a) f : x 2x+3 est la fonction affine de coefficients 2 et 3.
b) f(x) = -5x-2 est la fonction affine de coefficients
c) f(x) = 3-4x est la fonction affine de coefficients
d) f : x -6x est la fonction
Remarque :
Une fonction linéaire est