4 g ex etude fonctions

Lycée Rue Ahmed Amara Le Kef
Habib Gammar
Exercices (Etude de fonctions) 4
ème
EG
1/2
www.mathsplus.12r.org
Exercice 1
Soit f la fonction définie sur
{
}
\ 1
ℝ
par : 3
2
3 6
( ) ( 1)
x x
f x
x
− +
=−
( )
C
sa courbe représentative dans un repère orthonormé
( , , )
O i j
.
1) Montrer que f peut s’écrire sous la forme :
2
4
( ) 2
( 1)
f x x
x
= + + −.
2) On admet que le tableau de variation de f est le suivant :
x
−∞
1 3
+∞
f
+
∞
−∞
6
a) Calculer
1
lim ( )
x
f x
+
→
et
lim ( )
x
f x
→+∞
b) Montrer que la droite
: 1
D x
=
est une asymptote verticale à
( )
C
.
c) Montrer que la droite
: 2
y x
∆ = +
est une asymptote oblique à
( )
C
au
voisinage de +∞ et de −∞ .
d) Etudier la position relative de la courbe
( )
C
et la droite ∆.
3) a) Montrer que l’équation
( ) 0
f x
=
admet dans
ℝ
une unique solution α
b) Vérifier que
]
[
3, 2
α
∈ − −
.
4) Tracer dans le repère
( , , )
O i j
la courbe
( )
C
.
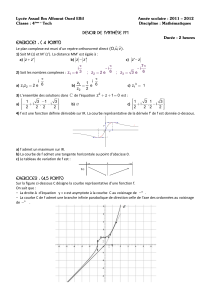
Exercice 2
Le plan est rapporté à un repère orthonormé
( , , )
O i j
.
La courbe
( )
C
représente une fonction f définie et dérivable sur
ℝ
.
• L’axe des abscisses est une asymptote à
( )
C
au voisinage de
−∞
.
•
( )
C
admet une branche parabolique de direction celle de l’axe des
ordonnées au voisinage de
+∞
Par lecture graphique :
1) Déterminer
(0) , (1) et '(0)
f f f
.
2) Déterminer
lim ( )
x
f x
→+∞ ,
lim ( )
x
f x
→−∞ et
( )
lim
x
f x
x
→+∞
3) Dresser le tableau de variation de f.

Lycée Rue Ahmed Amara Le Kef
Habib Gammar
Exercices (Etude de fonctions) 4
ème
EG
2/2
www.mathsplus.12r.org
Exercice 3
Soit f la fonction définie sur
ℝ
par :
2
3
1 1
( )
3 3 1
x si x
f x
x x si x
− ≤ −
=
− + + > −
( )
C
sa courbe représentative dans un repère orthonormé
( , , )
O i j
.
1) Etudier la continuité de f à droite et à gauche en −1.
2) a) Etudier la dérivabilité de f à gauche en −1.
b) Interpréter graphiquement le résultat.
3) Montrer que f est dérivable sur
{
}
\ 1
−
ℝ
et calculer
'( )
f x
.
4) Montrer que le point
(0,3)
Iest un point d’inflexion de
( )
C
5) Ecrire une équation de la tangente à
( )
C
au point I
6) Montrer que l'équation
( ) 0
f x
=
admet une solution
]
[
2,3
α ∈
.
Exercice 4
Donner la primitive F de f sur un intervalle I dans chacun des cas suivants
1)
2 3
( ) 1 3
(1) 0
f x x x x
F
= − + −
=
2)
2
1 1
( ) 2
(1) 1
f x x x
x
F
= − +
=
3)
4 2
2
( ) 3 2
4
(0) 2
x
f x x x x
F
= + − +
+
=
Exercice 5
 La courbe
( )
C
ci-dessous représente une fonction f définie sur
ℝ
.
 La droite T est la tangente à
( )
C
au point d’abscisse (−1).
lim ( ) 1
x
f x
→−∞
=
et
lim ( ) 1
x
f x
→+∞
= −
Par une lecture graphique :
1) Déterminer
(0) et '(0)
f f
.
2) Déterminer
1
( )
lim
1
x
f x
x
−
→
−
et
1
( )
lim
1
x
f x
x
+
→
−
3) Déterminer :
'( 1)
f
−
.
4) Donner une équation de la tangente T.
5) Dresser le tableau de variation de f.
6) Déterminer :
1
1
lim ( )
1
x
f
x
+
→
−
-2 -1,5 -1 -0,5 0,5 1 1,5 2O
-1
-0,5
0,5
1
( )
C
T